第0部分:一些废话
在CharlisのBlog遇到服务器跑路之前,原本第一篇的关于电机模型搭建的文章是写最基本的三相永磁同步电机的矢量控制模型的,但是吧,想了又想觉得三相模型属实是太基础了,本科阶段就已经基本解决了。况且在现在研究的双三相电机中,很多东西似乎大同小异。于是就针对我自己的研究方向——多相电机的控制,唠一唠双三相电机的矢量控制问题。
当然记录双三相永磁同步电机的搭建过程,一是记录自己研究方向的学习过程,方便常常温故知新;二是方便和老师同学相互交流讨论;最后也是为了丰富自己的网站咯哈哈哈哈(假装做个懂学术的研究生)。
本文介绍的电机均为永磁同步电机(Permanent Magnet Synchronous Motor——PMSM)
第1部分:绕组理论
双三相电机作为多相电机,首先介绍多相电机的绕组理论:
多相电机各相绕组的空间分布可以是对称的,也可以是不对称的。以六相电机为例,两种绕组结构如图1所示。图(a)是对称六相电机,相带角为60°,也可把它看成由两套相移 60°的对称三相绕组组成,称之为相移 60°双三相电机;图(b)为不对称六相电机,相带角变成了 30°。对称六相电机的绕组结构和传统 60°相带三相电机完全相同,其磁势空间分布和传统 60°相带三相电机是一样的。而不对称六相电机可以看成是 60°相带三相电机经裂相后得到,也就是每一个 60°相带拆成两个 30°相带,所以又可称为相移30°双三相电机,其磁势空间分布应该和对称十二相电机一致。
但是请注意,无论是图(a)的对称六相电机还是图(b)的不对称六相电机,都满足绕组的理想情况,即每一相绕组上的电阻和电感都相同。
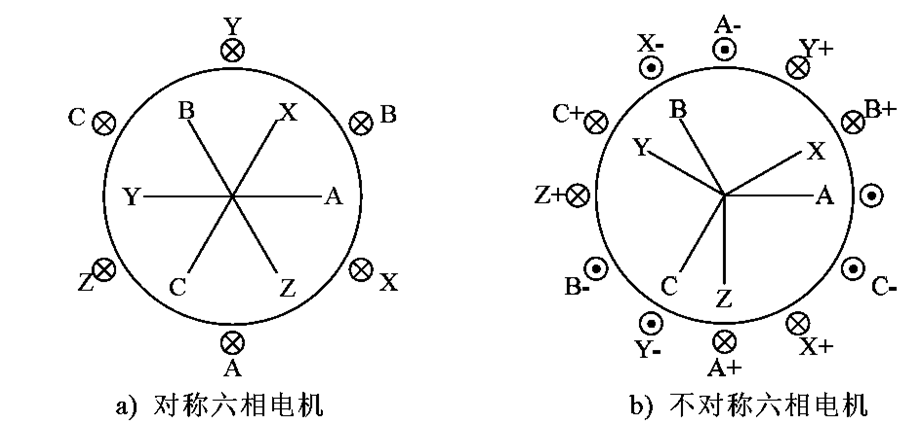
图1 六相电机的不同绕组分布图
以此理论为基础的其他多相电机不同绕组图如图2所示。其中,全对称绕组的中性点相连,但在半对称绕组结构中,各个三相绕组相互独立,即中性点不连接。
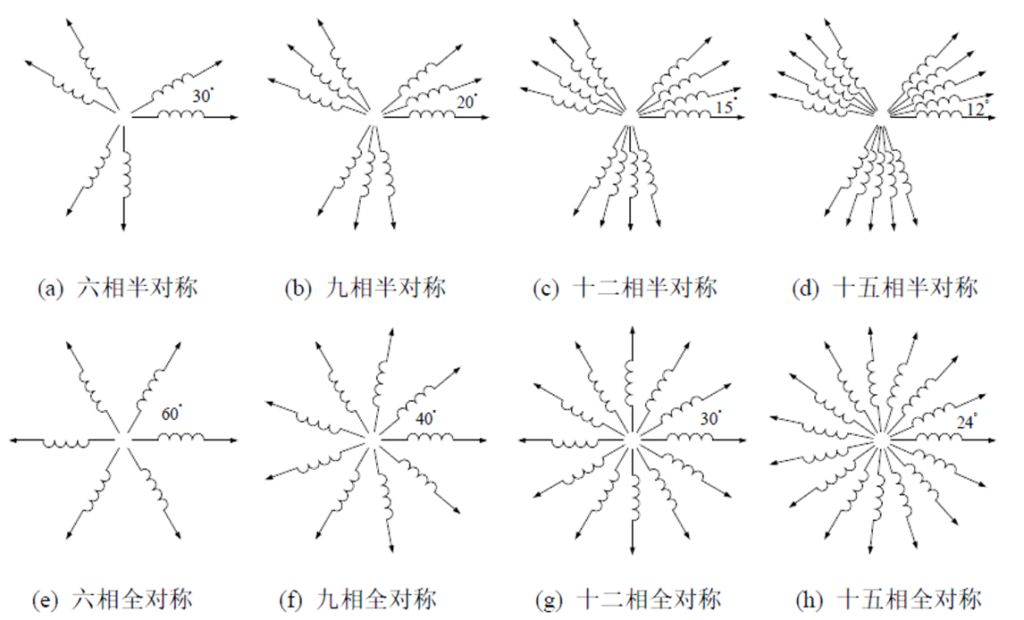
图3 多相电机绕组对称关系理论图
第2部分:电机数学模型
建立被控对象的数学模型是对控制系统进行分析和设计的基础。对高性能电机驱动系统而言,一个易于分析的电机动态模型更是不可缺少的。和普通三相电机一样,双三相永磁同步电机的建模过程也主要是一个坐标变换的过程。根据基本电磁原理和各相绕组之间的相对位置,可以很容易列出各相绕组电压、电流和磁链之间的关系表达式。
然而,这样所得到的模型往往过于复杂,具有高阶、非线性、强耦合的特点,给系统的分析和设计带来了很大的困难。通过选取合适的坐标系并进行坐标变换,可以将原始模型简化为易于分析的形式,因此建模的关键就在于如何选取新的坐标系。电机的矢量控制策略也和坐标系的选取具有紧密的联系,不同的坐标系对应着不同的矢量控制策略。
根据基本的电路和电磁感应原理,可以推导出电机中各变量之间的相互关系。为了简化分析,对电机作如下假设:(1)定子电流和转子永磁体产生的气隙磁链都作正弦分布;(2)忽略铁心磁饱和效应以及涡流、磁滞损耗;(3)忽略绕组之间的互漏感(与漏磁通相对应的互感系数);(4)转子上没有加入阻尼绕组。
双三相永磁同步电机电压和磁链基本方程分别为:
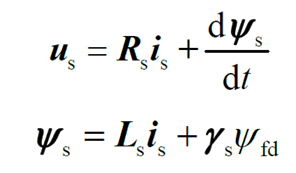
其中,
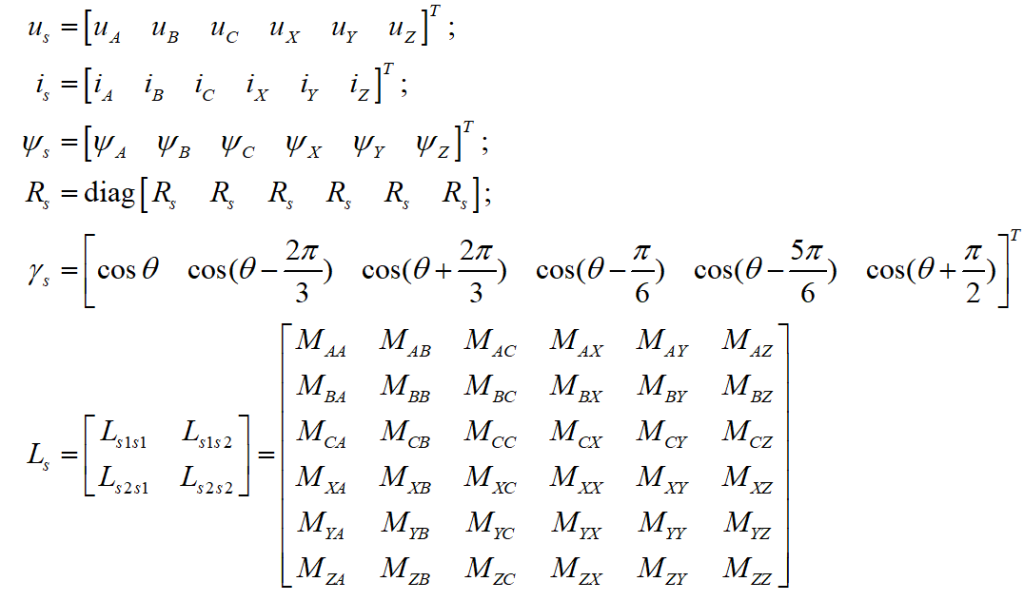
从机电能量转换的角度出发,六相PMSM的电磁转矩等于磁场储能对电机机械角度求偏导,可以得到:
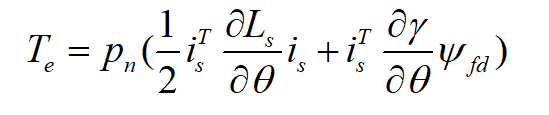
电机系统的运动学方程如下:
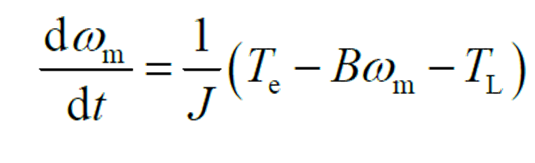
其中,us、is、Ψs分别表示相电压、相电流、相磁链矢量,单位分别为V、A、Wb。Rs、Ls别表示电阻、电感系数矩阵,单位分别为Ω、H。Ψs表示磁链系数矩阵,无单位。Ψfd为永磁体在每一相绕组中产生的磁链幅值,单位是Wb。
与三相电机相比,双三相电机的电感矩阵更为复杂。为了便于分析,将这些电感系数分成四组:Ls1s1表示第一套三相绕组内部的自感和互感;Ls2s2表示第二套三相绕组内部的自感和互感;Ls1s2和Ls2s1表示两套绕组之间的互感。θ为转子磁极位置与A相绕组轴线之间的电角度,单位是rad。
以矩阵Ls1s1为例,对角线上的MAA表示第一套绕组的A相对A相的自电感,MBB和MCC同理。第一行第二列的MAB表示第一套绕组的A相对第一套绕组的B相的互电感,MBA、MAC、MCA、MBC和MCB同理。
矩阵Ls1s2、Ls2s1和Ls2s2同理。其四个矩阵在本文中不再赘述。
第3部分:坐标变换
由于双三相电机本身是由两套绕组空间互差30°且中性点不相连的拓扑结构——空间上的存在实际是六相绕组,即ABC套绕组和XYZ套绕组,为了进行矢量控制,需要对其进行坐标变换:(为了更好的说明坐标变换,本部分包含机理部分和公式的推导)
ps.在对双三相电机进行坐标变换之前,需要先说明,双三相PMSM存在两种不同的建模方式:双dq模型和矢量空间解耦模型。这两种建模方式对双三相PMSM的建模效果是一致的,然而,双dq模型存在局限性(仅能针对三相、双三相或多三相PMSM进行建模,对如五相七相这种不是3的倍数的PMSM无法进行建模),因此本文主要针对通用性更广的矢量空间解耦模型进行讨论,接下来所述的部分也为基于矢量空间解耦模型的坐标变换:
采用矢量空间解耦的变换方法,将自然坐标系ABCXYZ的各个变量转换到静止坐标系的变换矩阵Tαβ为(该变换为双三相的Clarke变换):
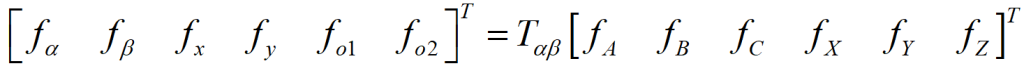
其中,变换矩阵Tαβ为:
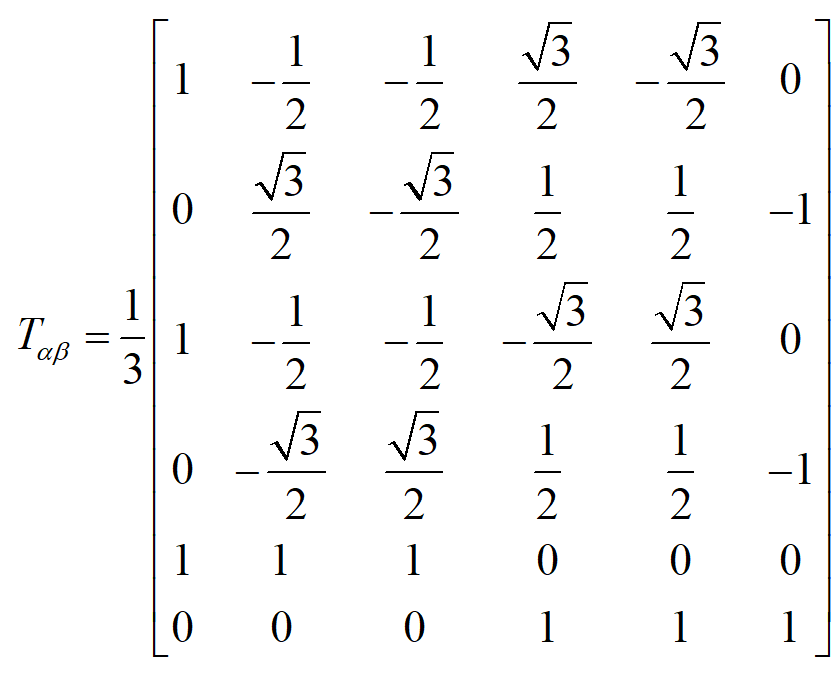
这里变换矩阵前的系数1/3是为了保证变换前后变量的幅值保持不变。如果以功率不变为约束条件,则该系数变为1/sqrt(3),该变换有如下特点:
①前两行对应了α-β子空间。电机变量中的基波分量和12k±1(k=1,3,5……)次谐波被映射到该子空间上,且能参与机电能量转化。
②中间两行对应x-y子空间。电机变量中的6k±1(k=1,3,5……)次谐波被映射到该子空间上,但不能参与机电能量转化。
③中间两行对应零序子空间。电机变量中的6k±3(k=1,3,5……)次谐波被映射到该子空间上,其属于零序分量,不能参与机电能量转化。
对于双三相PMSM来说,仅有α-β子空间的基波分量是实际参与到了电机的机电能量的转换中的,为了便于简化分析,将静止坐标系变换到同步旋转坐标系的关系式为:
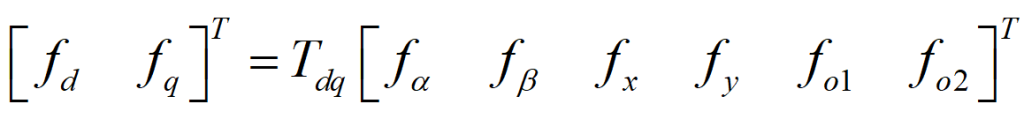
其中传统的变换矩阵Tdq通常为:
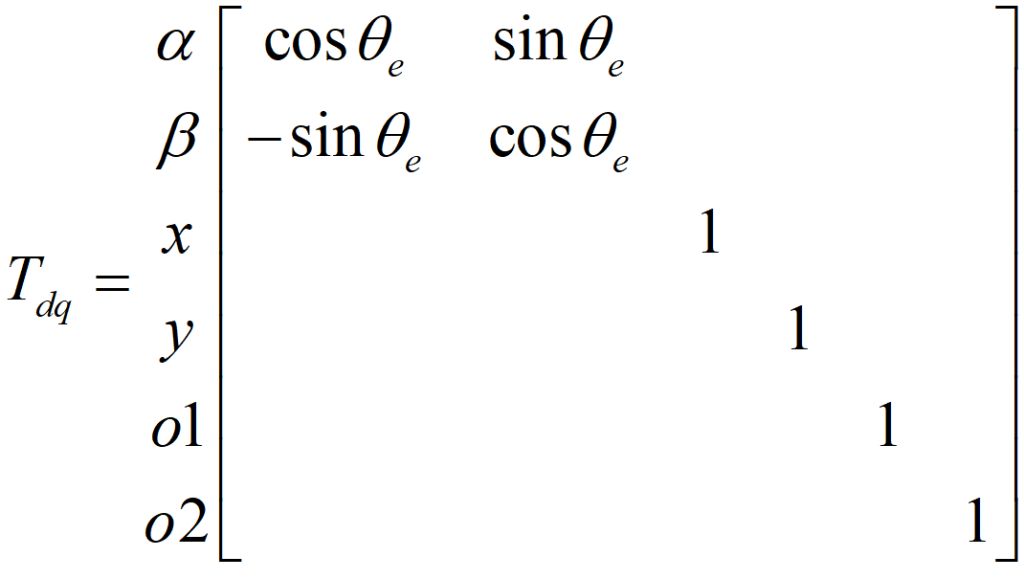
最后将自然坐标系变换换到同步旋转坐标系下的关系是为
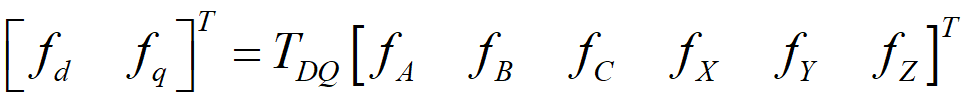
其中传统的变换矩阵TDQ通常为:
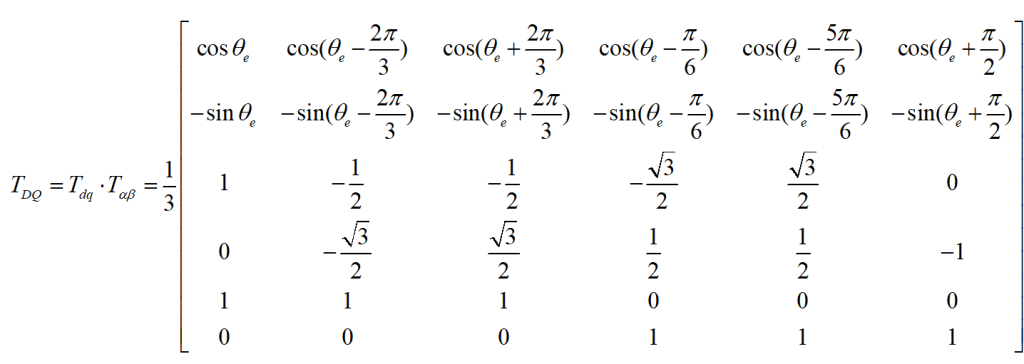
文献参考:
[1]杨金波.双三相永磁同步电机建模与矢量控制[D].哈尔滨:哈尔滨工业大学,2011.
[2]薛山.多相永磁同步电机驱动技术[D].北京:中国科学院研究生院,2005.
[3]杨金波,杨贵杰,李铁才.双三相电机的建模与矢量控制[J].电机与控制学报,2010,14(06):1-6




