前言部分:
似乎很久很久没有更新自己的Blog了……从六月初,到现在的十月底,遇到了很多人,碰上了很多事,更新Blog的事情就慢慢搁置下来了。最近和朱博靳博一起参加了数模竞赛,是第一次参加数模,也是最后一次参加(可能吧)。还是很有感慨的,于是乎记录一下。
至于为什么要参加竞赛,一来单纯觉得挺好玩的,二来感觉自己的研究生生涯居然也没有参加个什么比赛,思忖着也是丰富一下自己的生活,有点稀里糊涂的就参加的说。
经过讨论最后的选题是E题,身边的大家几乎不约而同选择的都是C题(主要也是C题比较贴合我们专业)。咱们是觉得选择开放性好一点的题目,最后不一定做出标准答案,会更好水一点(不是)。
E题:


这是一道开放性很强的题目。主要是针对高速公路拥堵的状况,视情况开启应急车道以缓解拥堵。题目给定了位于南京的一段高速公路的视频监控录像,从视频录像中挖掘信息——车流量、车流密度、车流速度等信息,通过建立一定的数学模型,判断未安装录像的区域的车流情况。
题目困难的一个点就在于,在给定的视频材料中提取关键信息,即上述的三个信息。由于视频是经过10倍速的,用双眼观察肯定是个办法,但是非常消耗时间。(但是后面我们真就用观察的方法进行的……)既然是数学建模的试题,肯定是要通过视频目标识别来进行的。这里感谢 @花开再相遇 提供的视频教程,使用Python里的一个Carcount的程序包,识别视频中的车辆,具体效果如图:
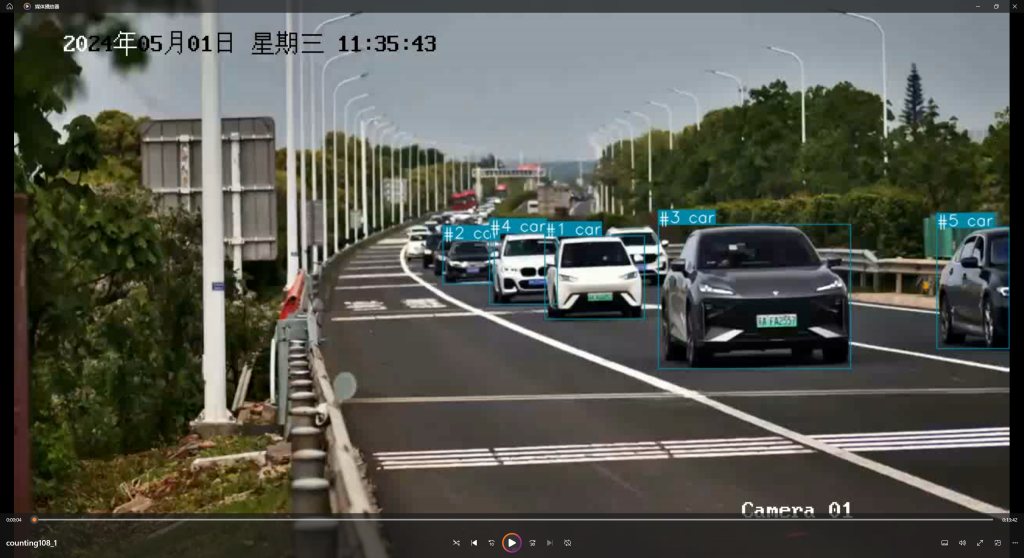
当程序每检测到一辆汽车时,计数count就往上+1。用该方法进行汽车的计数更加便捷,但是也有很大的弊端——首先就是由于车辆分布不均匀,很多车可能会由于视线被遮挡而导致程序提取不到,导致计数会变少;其次,由于视频是以十倍速进行播放,计数程序可能会出现跳帧计数,很多数字一下就跳过了,又导致计数变多了。所以用这个计数方法虽然很快,但是实际上非常不精准。不精准的数据对后续建模是有很大的影响的。所以后面其实摒弃了用程序计数的方法,还是选择了使用观察计数的方法。虽然时间上花费了有点多,但是为后续的准确建模进行了铺垫。
当然车流密度和车流速度最终还是使用了观察计数……
这个数据提取上由于没有经验,真的走了很多的弯路,导致第一天的做的工作到最后基本上全都废弃了,数据统计就进行了两天……
后续的建模也是困难重重——主要运用了LWR的交通流模型和拥堵模型结合道路疏通能力的建模来实现最终的建模。朱博运用了学习包的神经网络结合LWR来完善最终的建模。(不过感觉这个LWR的建模真的是预测能力太烂了,一点都不符合实际情况,只能说用来做题了。)
建模部分:
这里介绍一下建模:
参数说明:
由上述介绍,从视频材料中能得出三个最基本的信息:车流量、车流速度、车流密度。我们分别对其进行定义。
①车流量:
统计在每个时间间隔内通过观测点的车辆数,可以得到该时间段内的车辆流量。单位为量/分钟(veh/min)。本文中对于每个观测点,选定一个时间间隔Δt(一分钟)。在每个时间间隔内,统计通过该观测点的车辆数N(t,Δt),则流量为:
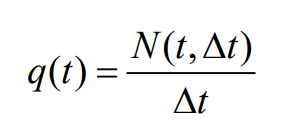
其中,N(t, Δt)是在时间间隔(t,t+Δt)内通过观测点的车辆总数,Δt 是时间间隔。
②车流密度:
车流密度是指在某时刻 t 上,单位长度道路上的车辆数,单位为辆/百米(veh/100m)。由于观测点只能捕捉到通过某一点的车辆信息,直接计算道路区间内的车辆数 n(t,L)可能有困难。为此,可以利用基本交通流理论中的流量-速度-密度关系,即:
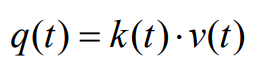
因此,可以推导出密度 k(t):
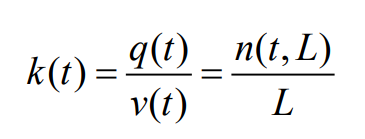
其中,n(t,L)是在 t 时刻,长度为 L 的道路区间内的车辆总数。(注:这个公式基于假设交通流是均匀的,即在短时间和空间尺度内,交通参数是连续和可微的。)
③车流速度:
对在时间间隔 Δt 内通过观测点的所有车辆,计算其速度的平均值,即得到该时间段内的平均车速。单位为米/秒(m/s)。通过视频数据,可以测量每辆车通过观测点时的速度 vi(t)。平均速度 v(t)表达式为:
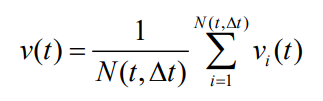
其中,vi(t)是第 i 辆车在时刻 t 通过观测点时的速度。
LWR模型建立:
LWR 交通流模型,全称为 Lighthill-Whitham-Richards 模型,是交通流理论中的一种重要的宏观模型。该模型由 Lighthill、Whitham 以及 Richards 于上世纪 50 年代提出,主要用于描述交通流的宏观动态特性。其最大的特点是能准确地描述交通流的动态特性,为交通规划、管理和控制提供有力的理论支持。
LWR 模型具体表达式如下式所示,公式满足交通流守恒定律,称为 LWR 交通流偏微分方程。
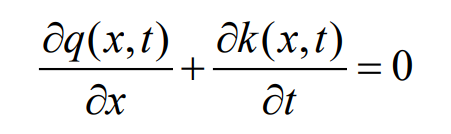
其中 q(x,t)为道路长度 x 在 t 时刻的流量,k(x,t)为道路长度 x 在 t 时刻的密度。
根据交通流偏微分方程建立动态交通模型,如下所示:
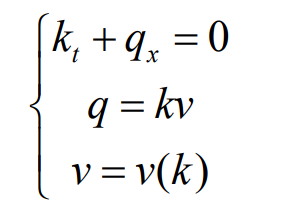
其中 kt 为密度对时间的偏导,qx 为流量对距离的偏导,v=v(x,t)是平均流速,结合以上公式,我们可以得到以下动态模型方程:
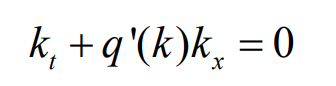
其中 q‘(k)=dq(k)/dk。
流速-密度关系我们使用一般流-密关系模型,通常情况下,流-密关系常常是用拟合经验数据来得到的曲线图,具有一般关系的 q-k 关系的 LWR 模型通常使用图解法来进行求解。
具有一般关系的流-密关系,通常是使用经验数据得到拟合曲线,其关系在下图中给出。
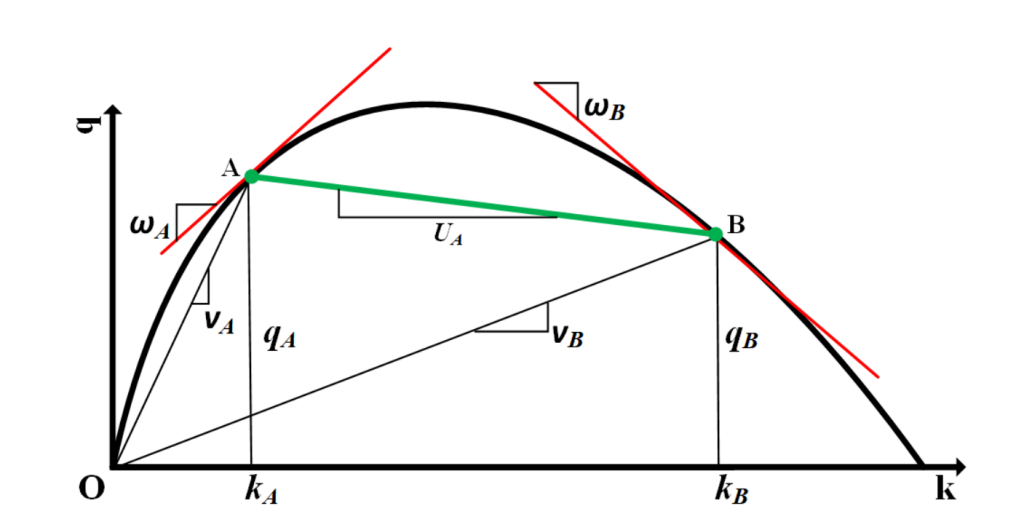
如上图所示,图中横坐标代表了车流密度 k,纵坐标代表了车流量 q。图中的点 A 表示了一种交通状况:车流量 Aq 、车流速度 Av 、车流密度 Ak 。B 的意义和标记同理。在该关系下,标记出初始条件。这是一个黎曼问题,每个运动波的速度(即特征线的斜率)都是常数,冲击路径将是一条直线。由初始条件可知,有两个运动波:从 x≤0 发出的波 A 和从x>0 发出的波 B。因为波 A 的速度是:
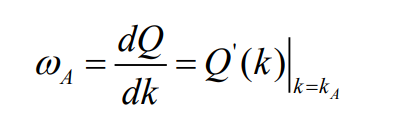
这是在 A 点处的 q-k 关系的导数,即 q-k 曲线上 A 点处的切线。因此,可以在 x≤0 范围内发出一组平行的、斜率为ωA的特征直线。B 点处的特征直线同理可得。
由于波 B 代表的是一队行驶在前的慢车队,而波 A 是一队行驶在后的快车队。快车队会赶上慢车队,即波 A 会赶上 B,从而形成冲击波。因为这是一个黎曼问题,冲击路径是一条直线,冲击波的速度由 Rankine-Hugonoit 的跃变条件所决定:
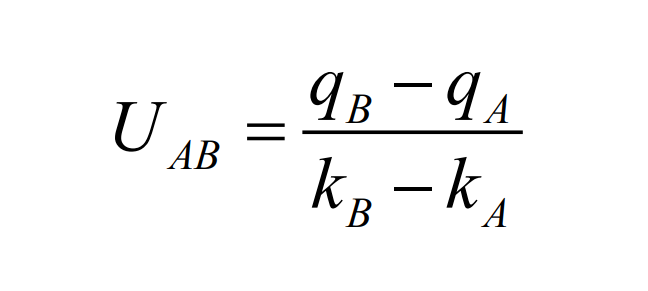
如下图所示,这个值恰巧是连接 q-k 曲线上点 A 和点 B 的弦的斜率。另外,根据初始条件我们已知冲击路径从时-空图的原点处开始,因此冲击路径就是从原点作的一条斜率为UAB 的直线。组成两个运动波的特征线都终止于冲击路径。这样,我们就用图解的方法画出了问题的冲击波解。
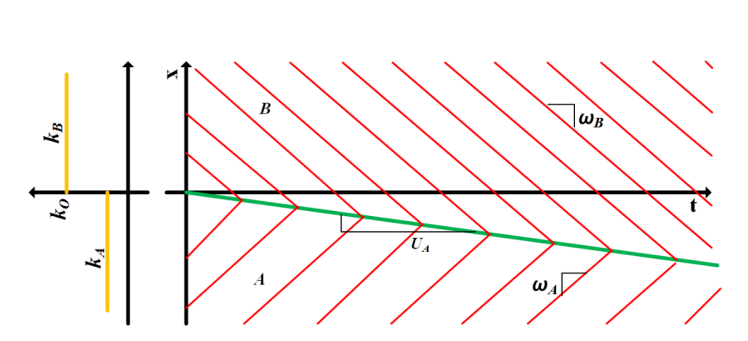
实验结果这里就不给出了,因为一般流-密关系的LWR交通流建模方式建立模型的偏差还是太大了,在路段内预测车辆运行速度相对非常不标准了。
基于拥堵系数的交通流模型建立:
如下图所示,本模型将基于改进的交通状态评价标准,作为应急车道开放决策模型中动态应急车道开放的先决条件。相比于传统的交通评价标准,改进的交通评价标准是针对于特定高速公路的拥堵评价标准,重新给定了高速公路在开通和禁用应急车道的不同的疏通能力参考,定义了疏通能力增益 α,并建立新的模型。
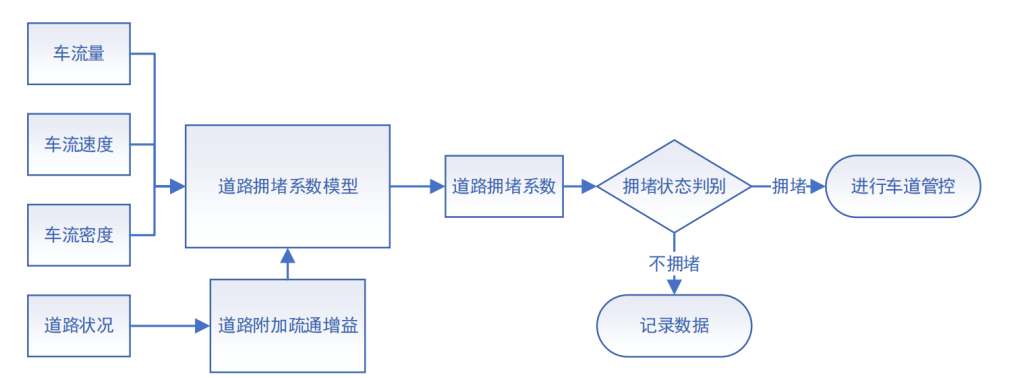
基于路段部分的车流量、车流密度、车流速度等信息,构建了交通状态评价算法,基本评价算法如下:

拥堵系数具体算法可以用数学方法来描述:
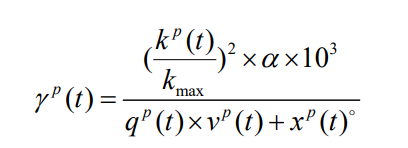
式中,γp(t)表示在地点 p 的 t 时刻对应的交通时段的拥堵系数;kp(t)表示在地点 p 的t 时刻对应的车流密度;kmax表示在当前路段范围内可以容纳的最大车流密度值;α 表示该路段的道路疏通能力,具体规则在下文中给出;qp(t)表示在地点 p 的 t 时刻的车流量;vp(t)表示在地点 p 的 t 时刻的车流平均速度;xp(t)。
表示若在地点 p 的 t 时刻发生绝对拥堵,即车流量qp(t)为 0,车流平均速度vp(t)也为 0 时,在公式分母添加无穷小,使拥堵系数γp(t)在该时刻为无穷大,表明该时刻绝对拥堵,车辆无法通行。
根据美国国家合作高速公路研究项目(The National Cooperative Highway Research Program)在 1995 年提出的现代城市规划道路理论模型中,车道宽度应至少大于车辆宽度的 25%。该理论既可以保证道路行车的安全,不易发生交通事故,又可以让这些剩余空间在道路发生拥堵的情况下发挥一定的疏通作用。即在发生拥堵的情况下可以通过车辆腾挪,使道路中的剩余空间可以得到最大的利用。根据道路附加的疏通能力模型,经过改进后得到其新的模型为:
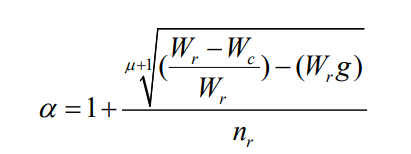
式中,Wr表示道路单车道宽度;Wc表示行驶在该道路上的轿车的平均宽度;nr表示当前正在使用的车道数;g 为增益调节系数;μ 表示该条道路的路面情况,即每平方米能使用的路面占总路面的比例:
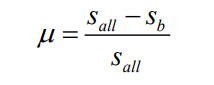
式中, sall表示单位总面积,sb表示单位面积中崩塌的路面面积,即不可使用的路面面积。
鉴于高速公路路面情况良好,sb在本模型中取取 0,μ 在本模型中取为 1。由附加的道路疏通模型,根据国家高速公路路面宽度和小轿车的平均车宽,计算出在不同车道下的疏通附加增益 α,并将该附加增益在车道数等于 3 的情况下进行归一化处理,得到下表的数据。

在对拥堵路段判断完成,判别是否启用应急车道时,本章所用的方式是决策者对比两车道的拥堵系数和开启应急车道后的拥堵系数的差值,来判断是否开启应急车道。
启用应急车道后的两车道高速公路可以视为普通的三车道路面,其道路容量kmax和疏通能力 α 有了一定的提高,因此,开启应急车道后的道路拥堵系数会有明显的下降。现给出如下定义:
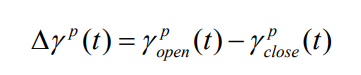
式中, γpclose(t)表示在该模型中,关闭应急车道的情况下在地点 p 的 t 时刻对应的交通时段的拥堵系数;γpopen(t)表示在该模型中,开启应急车道的情况下在地点 p 的 t 时刻对应的交通时段的拥堵系数;Δγp(t)即为应急车道开启前后交通时段拥堵系数的差值。
决策者通过实时监测高速公路道路上的车流量、车流密度、车流速度等参数,参考应急车道开启阈值的大小,决策是否启动应急车道。
经过给定视频材料的数据计算,本章推荐在某一时间区间内,关闭应急车道的情况下的γpclose(t)大于 1 的时间占总时间的 75%且拥堵系数差值Δγp(t)大于阈值 0.5 的时间也占总时间的 75%时,决策者宜开放应急车道,以减小车流密度,避免路段阻塞。
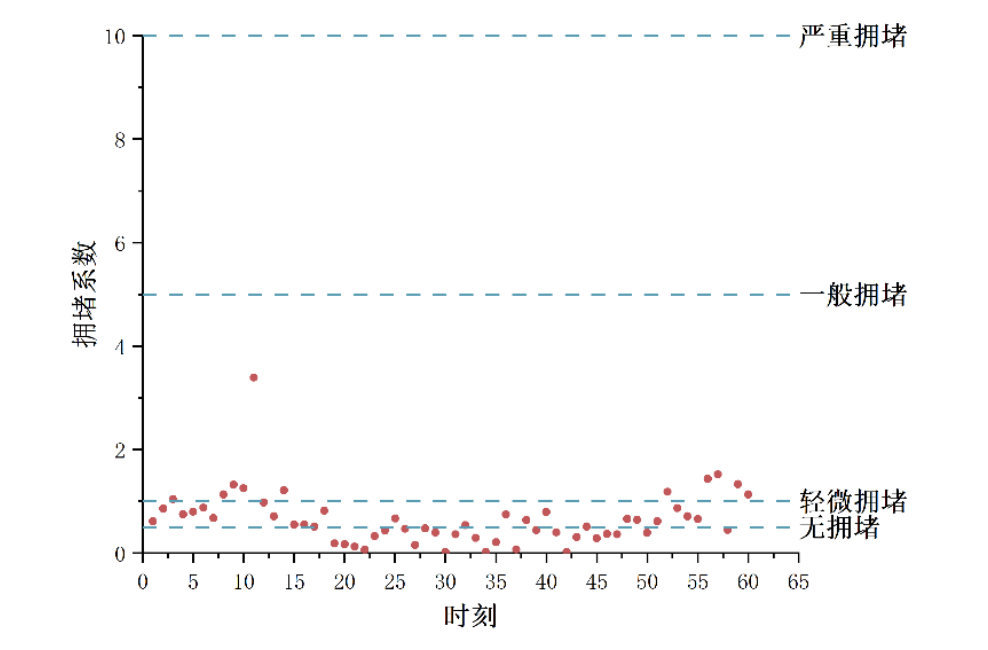
上图为某观测点的拥堵系数点分布图
根据所给定的决策依据,该路段γpclose(t)大于1 的总时间并未达到总时间的 75%。因此,该路段尚未出现拥堵情况,建议决策者关闭应急车道。
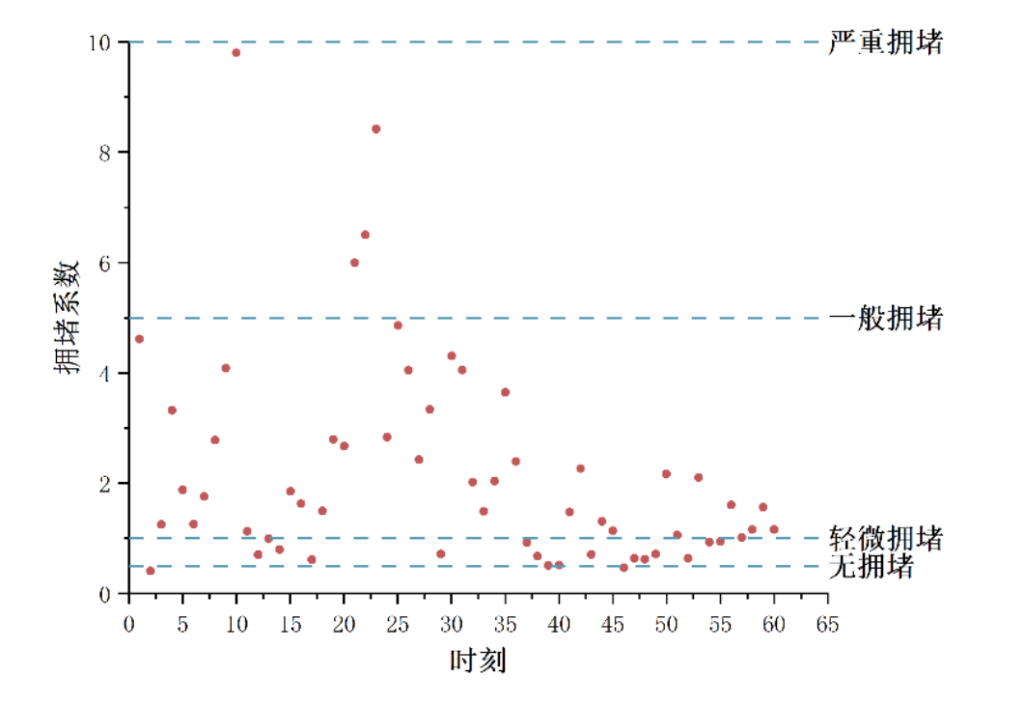
同样的,如上图所示为另一观测点的拥堵系数点分布图,根据所测得的数据,结合拥堵系数模型计算,我们发现在该观测点的拥堵系数离散程度较大,且该观测点的拥堵系数基本处在大于 1 的区间内,即道路状态处在一般拥堵下,部分时刻道路处在严重拥堵的状态下。
根据所给定的决策依据,该观测点所在的路段γpclose(t)大于 1 的总时间并已经达到总时间的 75%,因此对该路段应急车道开启阈值Δγp(t)进行计算。拥堵系数差值Δγp(t)随时间变化规律如下图所示。
根据所给定的决策依据,在给定的时间区间内,该路段关闭应急车道的情况下的γpclose(t)大于 1 的时间占总时间的 75%且拥堵系数差值Δγp(t)大于 0.5 的时间也占总时间的 75%。
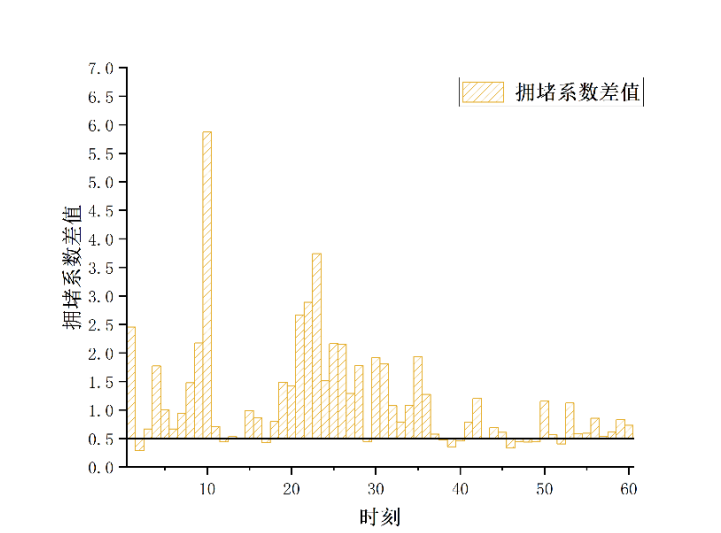
因此,该路段已经出现拥堵情况,建议决策者开启应急车道。
基于BP 神经网络模型建立与求解
该部分主要是朱博进行的,基于PEIT学习包中的BP神经网络模型,然后通过已给模型进行机器学习。
由于这部分我没有过多参与,Blog中也不过多解释咯。
小结:
参加数模竞赛真的是临时起意,抱着重在参与的心态尝试了一下(毕竟以后再不参加就真的没有机会了——研三应该没空参与咯)。在四天的时间内,和朱博靳博一起思考问题解决问题,在108奋斗到凌晨两三点,也是非常宝贵的一段经历了。



