【本文最后更新时间：2025.2.27】
第0部分——一些废话
在Charlis的Blog中，电机理论部分是很久很久没有更新过了！是一直停滞在了双三相电机的矢量控制部分。并不是研究只进行到了矢量控制啦，而是比较懒的没有及时更新下去。
后续其实一直有在研究下去双三相永磁同步电机的控制，主要是硬件拓扑结构的转换——利用九开关逆变器驱动双三相电机，并尝试进行绕组开路故障的容错控制（这部分后续肯定会更新，因为真的耗费了我很大的精力），但是由于存在拓扑结构本身的缺陷，导致容错控制这块并不能理想的呈现，因此在老师的建议下，我还是将课题更换为了理论上更加可行的中性点供电拓扑控制的三相永磁同步电机驱动的研究上面来。
第1部分——概述
在写本篇的过程中，就先默认读者已经了解了三相(双三相)永磁同步电机的驱动原理（如果并不了解，后续在更新双三相的部分中会再次介绍的），那么下面直接介绍课题内容：
如图1所示是三相两电平逆变器驱动的三相永磁同步电机拓扑结构。我们可以看到，电机中性点N并未被使用到，逆变器前端的直流母线电压完全由电源提供。由于电机所需的功率较大，而电驱系统对电池组的体积，重量有严格限制，因此一般使用低压电源加DC/DC升压变换器的组合形式来作为直流母线电压的输入。
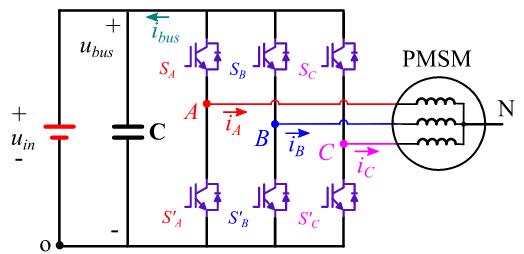
如图2所示，为使用低压电源外加DC/DC升压变换器组合作为直流母线输入的拓扑结构——
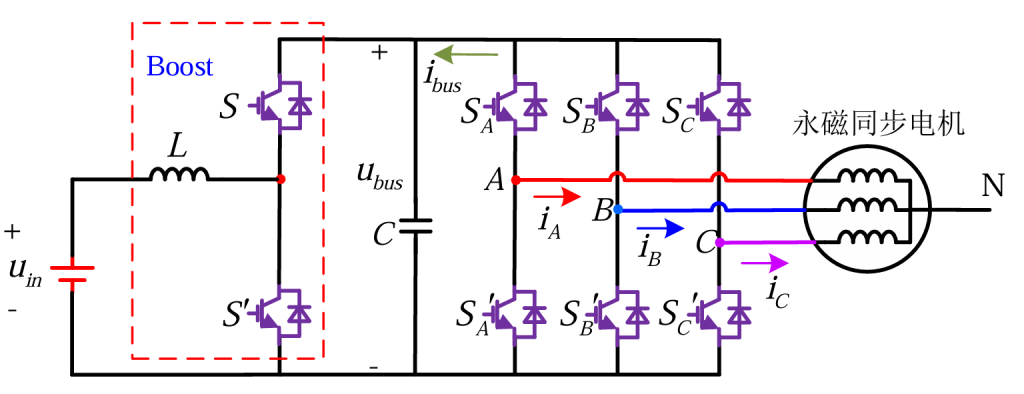
然而使用额外的DC/DC升压变换器，一来并没有减少多少体积，二来DC/DC升压变换器是增加了额外的功率器件，增大了系统的能耗而且增大了系统的不可靠性，因此提出了中性点供电的三相永磁同步电机拓扑结构，如图3所示。
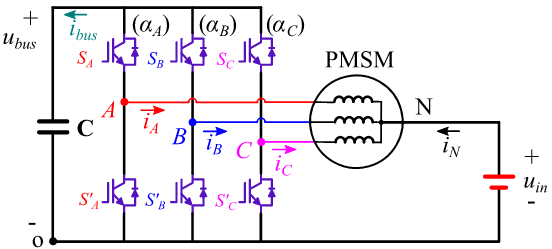
中性点供电拓扑结构的关键在于分别为电机和直流母线电压找到控制自由度。通过零序电压补偿策略，中性点供电拓扑结构可以同时驱动电机和调节直流母线电压。
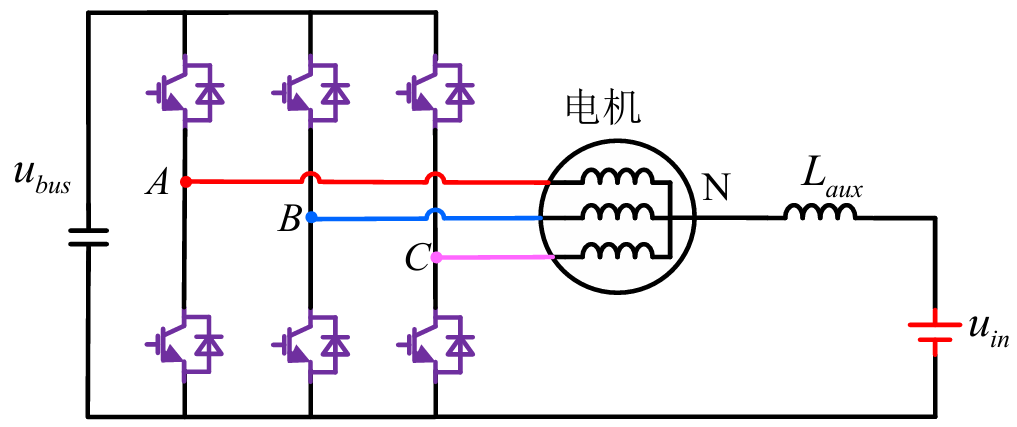
中性点供电的三相电驱动系统中过大的电流纹波会在电机中产生更多的铁损耗，从而降低整个驱动系统的运行效率，为了电流纹波，有学者提出了在中性点处串入电感的结构，如图4所示。增加的串联电感实际上增加了零序回路的等效电感，串联的电感越大，电流的纹波就越小。因此，使用串联电感可以减少零序回路中的电流纹波。
第2部分——中性点供电拓扑建模
2.1 永磁同步电机数学模型
永磁同步电机数学模型包含了四组方程——电压方程、磁链方程、电磁转矩方程和运动方程。（本来想把电机数学模型省略了，但是发现blog中还没有写过三相永磁同步电机的数学模型，就在这里简单补充一下咯）为了简化分析，假设三相永磁同步电机为理想电机，且满足下列条件：
① 忽略电机铁芯的饱和；
② 不计电机中的涡流和磁滞损耗；
③ 电机中的电流为对称的三相正弦波电流。
这样，自然坐标系下永磁同步电机的三相电压方程（2.1.1）为：
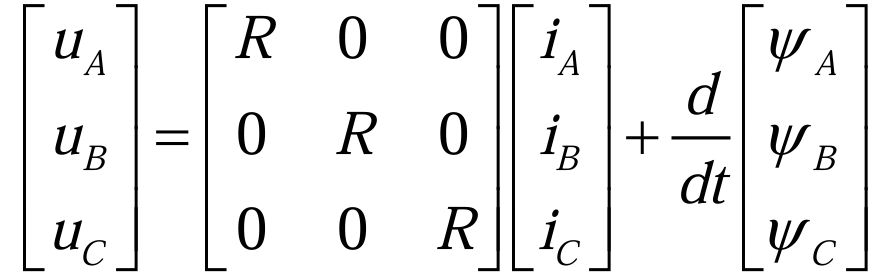
其中，UA、UB和UC是永磁同步电机的相电压，R为定子绕组，iA、iB和iC是相电流，
A、B和C是三相绕组上的磁链。
磁链方程（2.1.2）为：
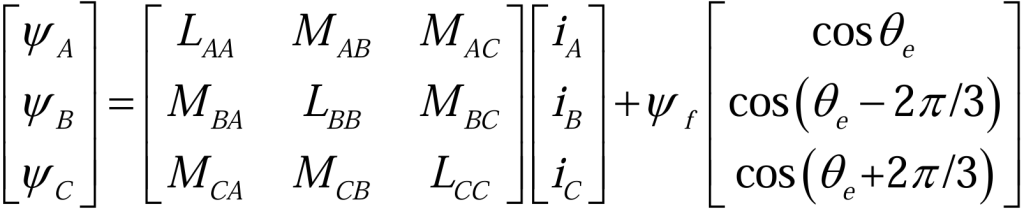
其中，LAA、LBB、和LCC是各相绕组自电感，MAB、MAC、MBA、MBC、MCA和MCB为绕组之间的互电感，f是永磁体磁通，
sh是电机转子的电角度。
电磁转矩方程（2.1.3）为：
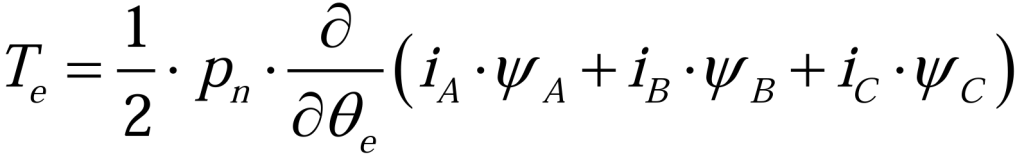
其中，Pn为三相永磁同步电机的极对数。
运动方程（2.1.4）为：
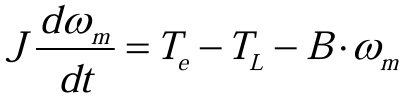
其中，
we为电机的机械角速度，J为转动惯量，B为阻尼系数，TL为负载转矩。
由4个电机数学模型公式可以看出，三相永磁同步电机的数学模型是一个比较复杂且强耦合的多变量系统。
2.2 平均模型
对图3所示的基于中性点供电拓扑的永磁同步电机驱动系统，采用平均建模法，推导对应的平均模型。将一个PWM周期内变量均值定义（2.2.1）为：
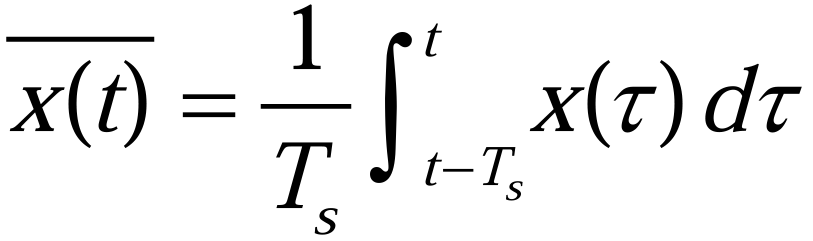
对于逆变器部分，假设开关频率足够高以忽略电流波动，并且忽略开关管上的电压降和死区时间，则稳态下，图3拓扑结构的平均电压方程（2.2.2）为：
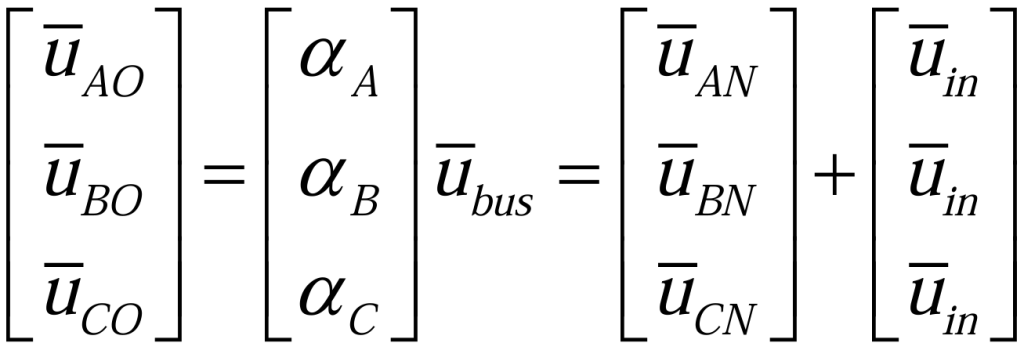
母线平均电流方程（2.2.3）为：
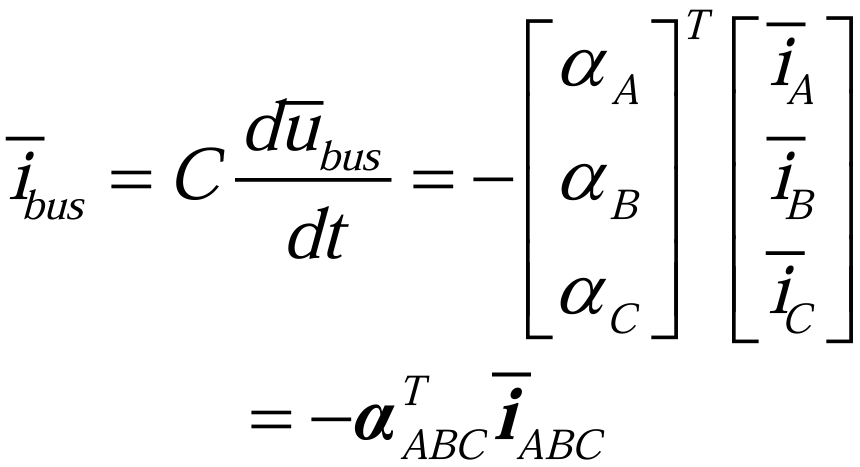
其中，αA、αB和αC分别是SA、SB和SC对应的占空比。由基尔霍夫电流定律，对于电机的中性点N，存在（2.2.4）：
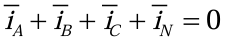
根据等幅值的克拉克变化和帕克变化，通过变换矩阵Tp（2.2.5）:
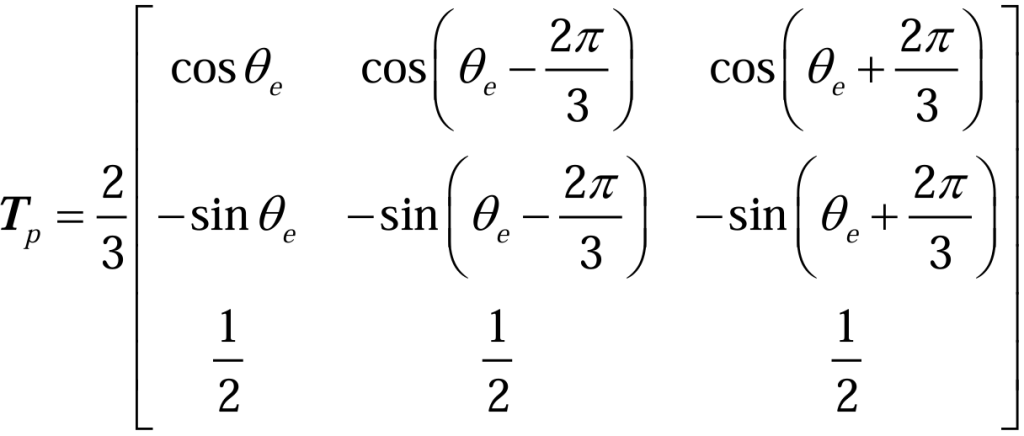
将平均电压方程从自然坐标系变换到同步旋转坐标系下，可以得到(2.2.6):
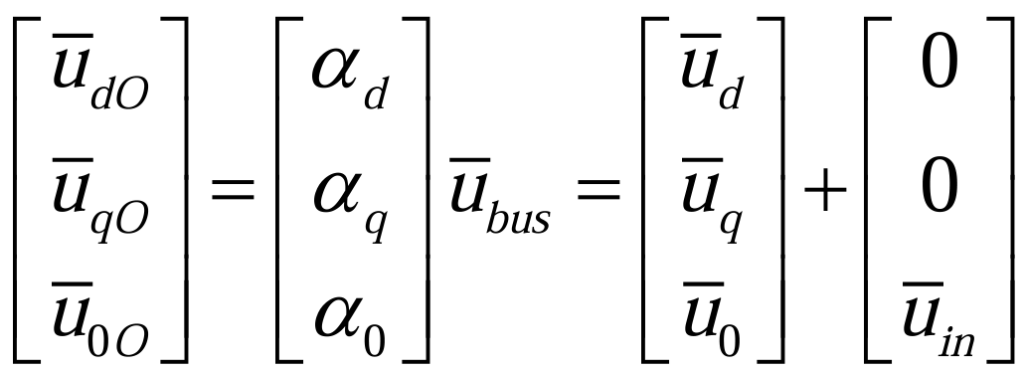
根据公式（2.1.1）（2.1.2）（2.2.5），代入三相永磁同步电机的定子方程中，并表示在旋转坐标系下（2.2.7）：
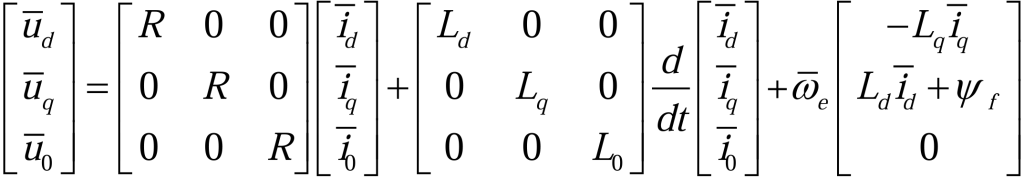
将公式（2.2.7）代入到公式（2.2.6），则零轴项（2.2.8）变为：
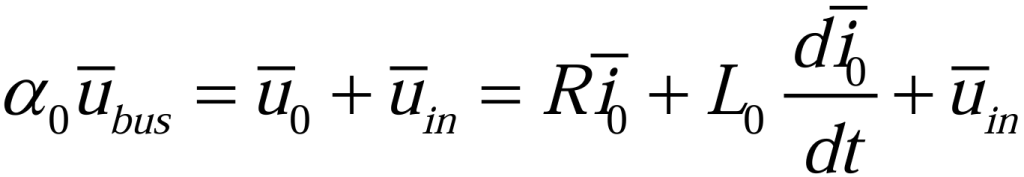
根据（2.2.5）（2.2.2）和（2.2.4）可以得到（2.2.9）和（2.2.10）：
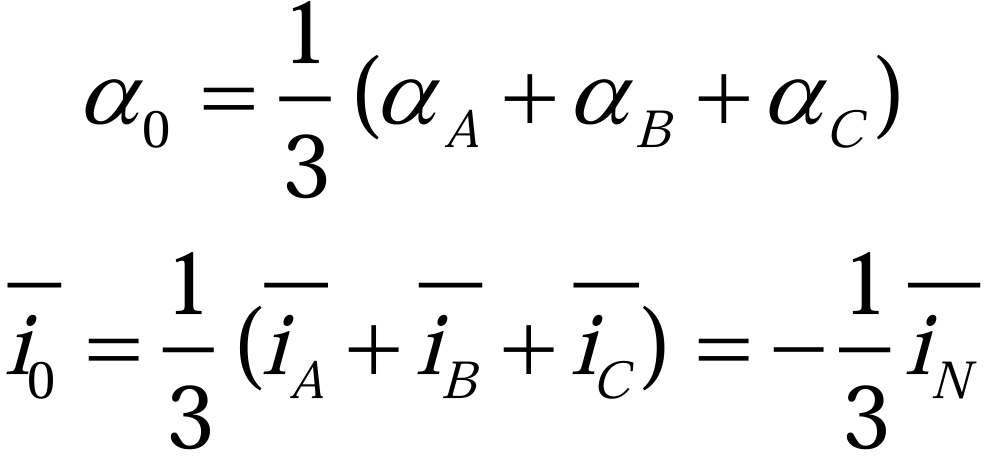
将（2.2.9）和（2.2.10）代入到（2.2.8）得到（2.2.11）：
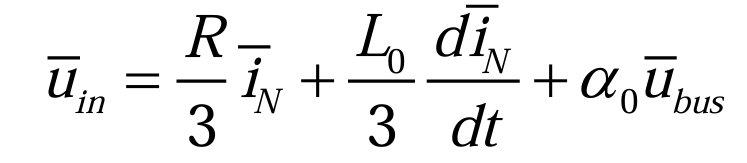
由于A、B和C三相占空比的取值范围为0到1，因此0轴占空比也是限定在了0到1之间，定义逆变器的平均占空比
H定义（2.2.12）为：
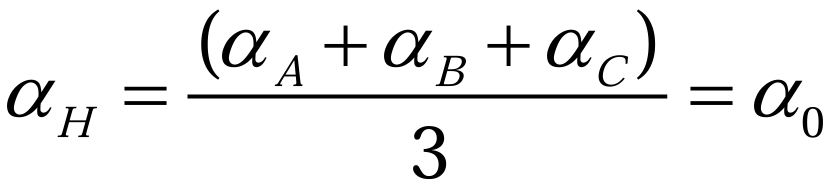
将（2.2.12）代入（2.2.11）得到（2.2.13）：
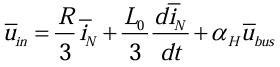
由（2.2.13）不难看出，在稳态情况下忽略寄生电阻上的压降，可以得到Ubus≈Uin/H，即中性点供电拓扑结构的稳态升压比为1/H。
2.3等效电路
根据（2.2.13），可以得到基于中性点供电拓扑的永磁同步电机驱动系统的等效电路为：
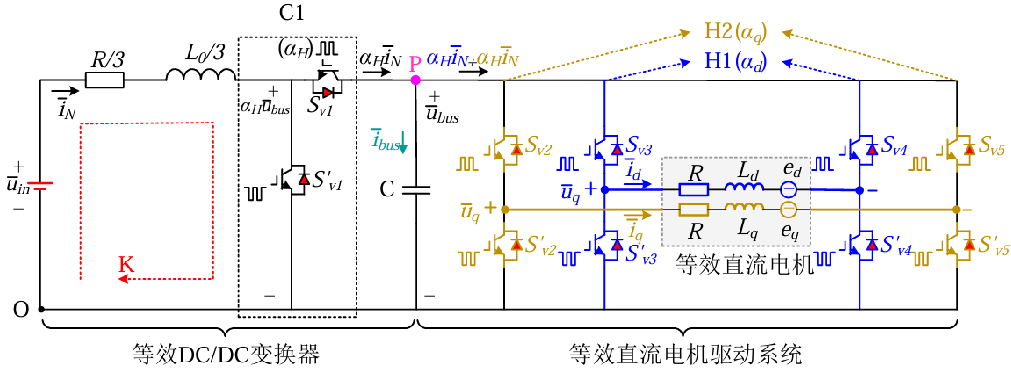
将一个DCDC变换器定义为“C1”，将两个H桥定义为“H1”和“H2”，可以将基于中性点供电拓扑的永磁同步电机驱动系统转换为级联的DCDC变换器——直流电机驱动系统。图中，需要说明的是：
①开关Svn和Svn‘(n=1、2、3、4、5)信号互补，且H为Sv1的占空比；d表示Sv3和Sv4的占空比之差；q表示Sv2和Sv5的占空比之差。
②回路K表示了方程（2.2.13）的电压关系。
③双H桥表示了（2.2.6）、（2.2.7）中的电压关系。
因此，等效电路明确揭示了基于中性点供电拓扑永磁同步电机驱动系统存在等效DC/DC变换器的功能，并且永磁同步电机可以视为等效DC/DC变换器的负载。同时，它还揭示了电机和等效DC/DC变换器在d-q-0坐标系中是解耦的，因此H可以作为等效DC/DC变换器独立的控制变量。
第3部分——控制部分
3.1电机电流环与转速环控制
电机电流环控制和转速环控制是使用PI控制器进行控制，详细内容见“PI控制器参数的调节方法整理”，在此不再过多描述了。
3.2直流母线电压控制
根据推导出的基于中性点供电拓扑永磁同步电机驱动系统的等效电路，可以将永磁同步电机视为等DC/DC变换器的等效负载RLoad。因此，图5可以化简为如下的图6。
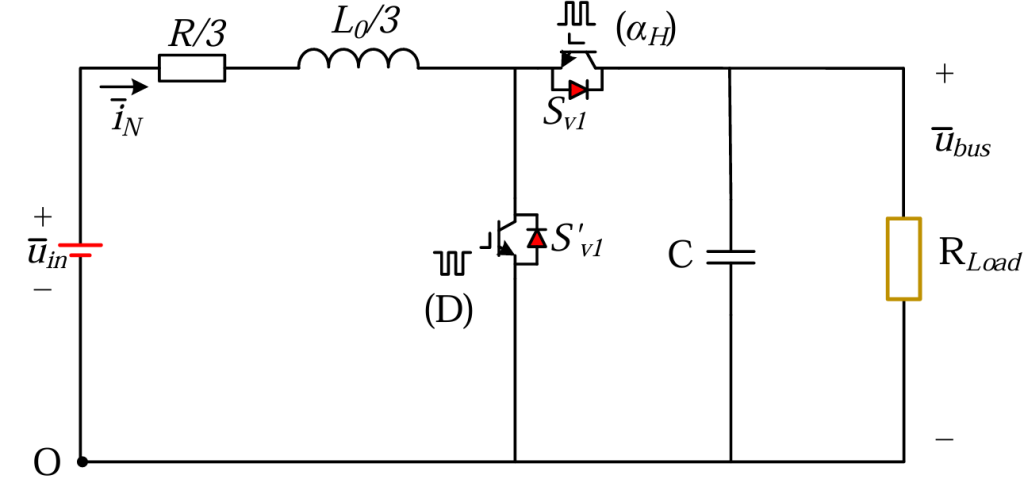
D表示Sv‘的占空比，忽略死区时间后，H=1-D。在不考虑损耗的情况下，RLoad可以近似计算为（3.2.1）：
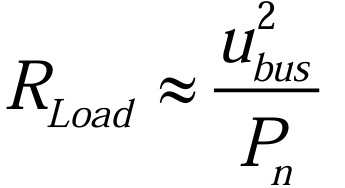
其中，ubus表示直流母线电压，Pn表示额定功率。稳态时电路满足（3.2.2）：
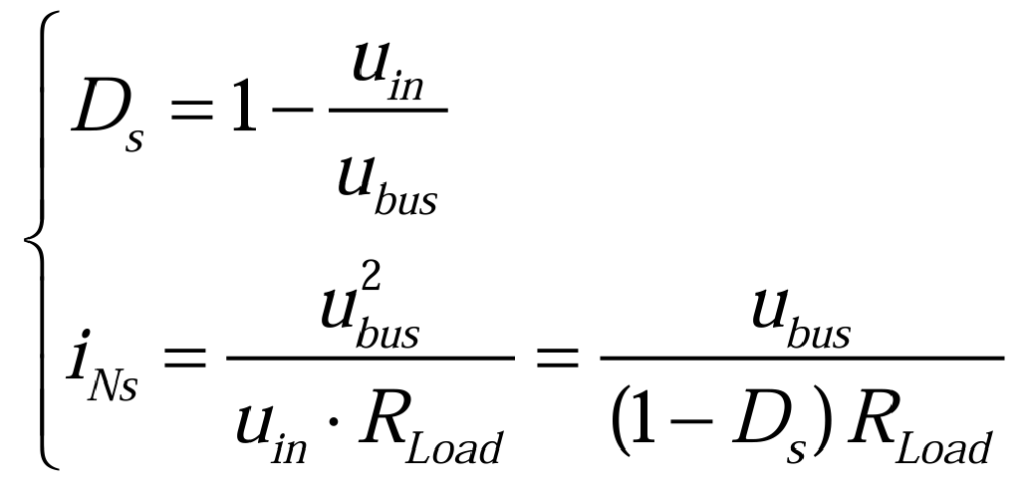
由于存在开关管，DCDC变换器在其导通和关断的时候是两种不同的开关状态，因此电感电容上的微分方程是会发生变化的，它是时变系统。PWM系统的输入是实时采样的模拟量，输出为数字量，呈现非线性关系。因此整个DCDC变换器是非线性时变系统，我们需要用到建立交流小信号线性模型的方法。
针对图6，得到Ton(Ds闭合)时的等效电路图：
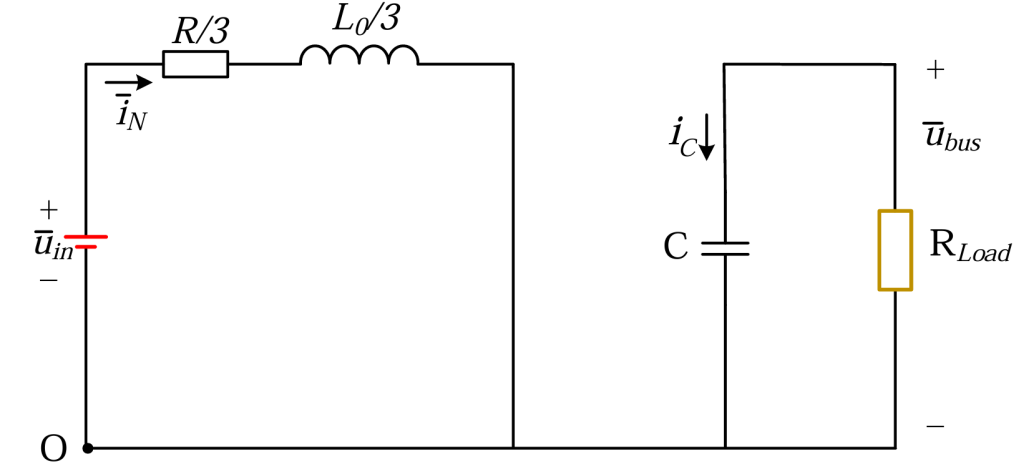
忽略电阻上的压降，由基尔霍夫电压、基尔霍夫电流定律，可以得到（3.2.3）：
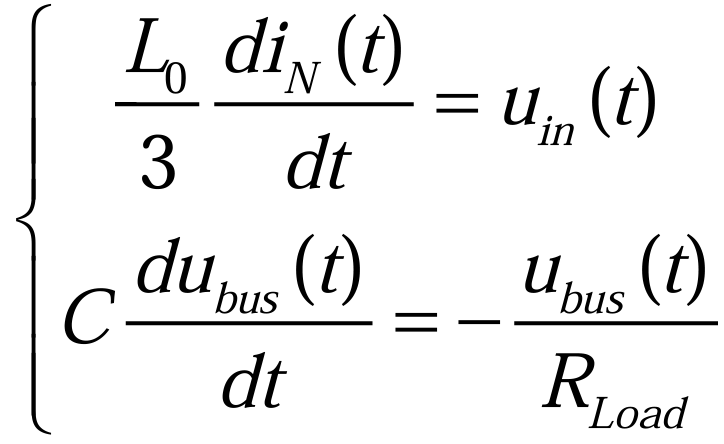
针对图6，得到Toff(Ds打开)时的等效电路图：
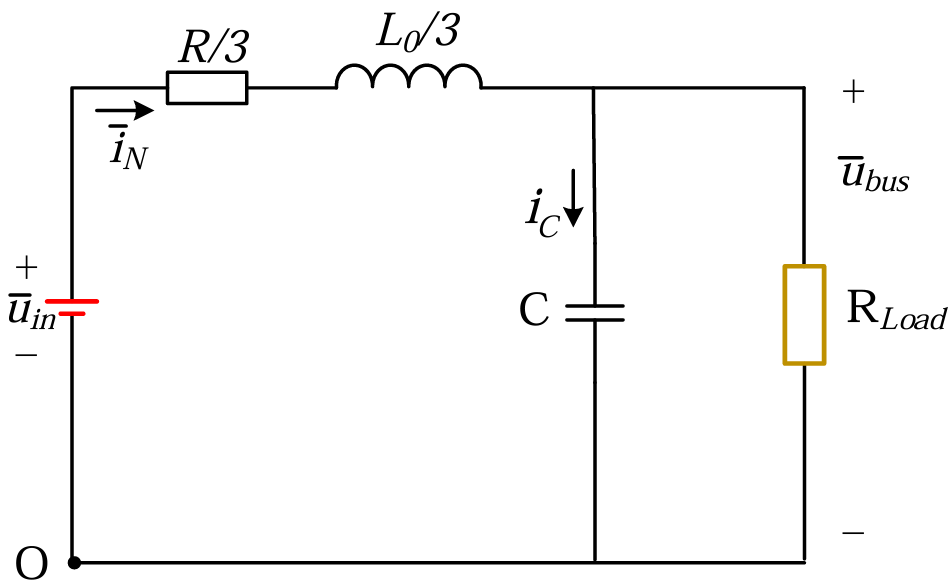
忽略电阻上的压降，由基尔霍夫电压、基尔霍夫电流定律，可以得到（3.2.4）：
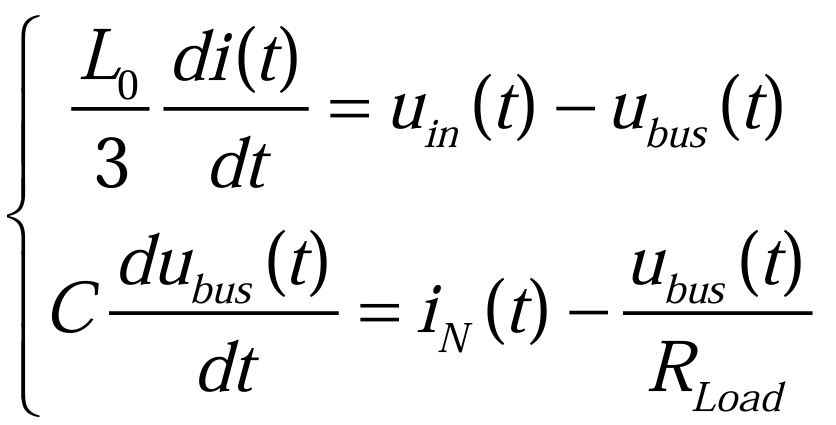
引入开关函数q（t），表示任意时刻的开关状态（3.2.5）：
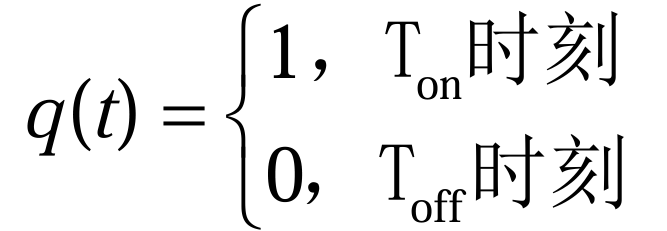
则利用（3.2.5）将导通(3.2.3)和关断状态(3.2.4)的电路表达式可以合并为（3.2.6）和（3.2.7）：
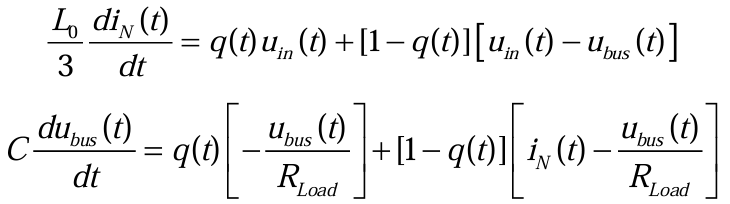
但开关函数q(t) 本质上还是时变变量，因此引入平均变量。周期平均变量的表达式如公式(2.2.1)所示，对开关函数q(t) 取平均值，可得(3.2.8)：
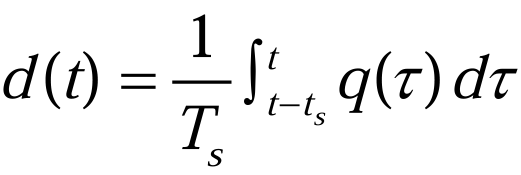
从q(t)到d(t)，本质上就是完成了时变到非时变的转化，d(t)表示了在一个周期内的开关管的平均占空比。同理，对电感电流、电容电压求平均，完成时变到非时变的变换，可得（3.2.9）和（3.2.10）：
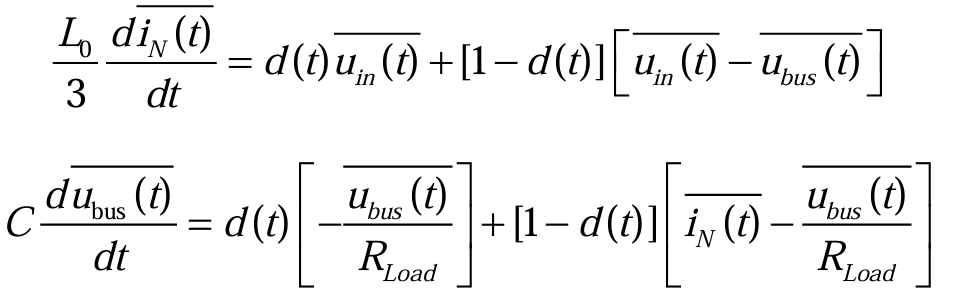
对时变量取平均值，尽管方程还是非线性的，但是可以在DCDC稳态工作点附近看作是一个线性系统。由自动控制原理可以得到，通过引入小信号扰动，将非线性方程作线性化处理。稳态工作点如式（3.2.2），在稳态工作点附近引入微小扰动（3.2.11）：
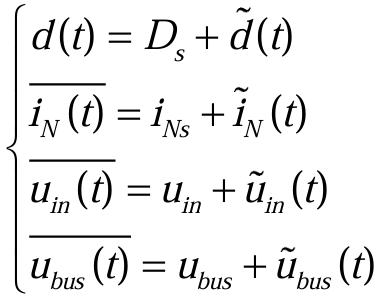
带波浪线的是小信号扰动，代入（3.2.9），得到（3.2.12）：
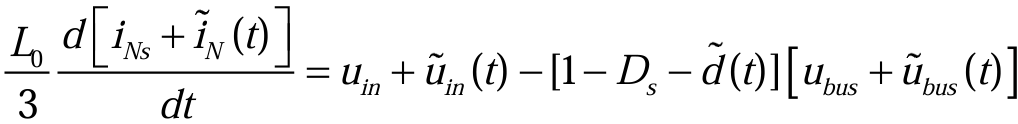
将（3.2.12）展开，方程左右两边交流项等于交流项，则（3.2.13）：
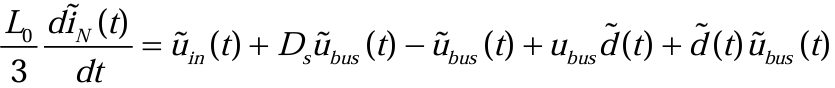
保留满足线性关系的一阶交流项，忽略二阶非线性交流项，得到线性化的电感电流方程如下（3.2.14）：
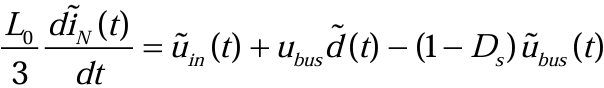
同样的，对（3.2.10）进行处理，得到（3.2.15）：
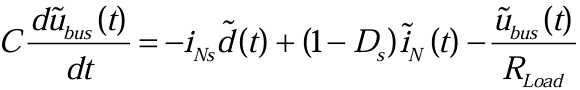
推导DCDC变换器的传递函数时，一般会选择忽略输入电压的小信号扰动，主要目的是为了简化模型，优化控制策略，以及适应实际应用中输入电压的稳定性。忽略输入电压的小信号变化可以避免模型过于复杂，有助于清晰地评估控制输入变化(如占空比)对系统性能的直接影响，从而清晰地看到控制策略的效果，并且更容易地设计和优化控制器。
因此，对（3.2.14）进行简化，简化后的电感电流方程为（3.2.16）：
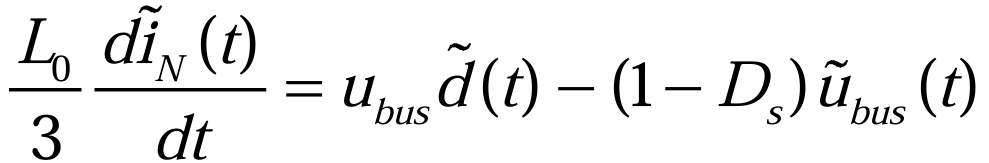
将（3.2.15）和（3.2.16）结合写成矩阵方程形式，可以得到（3.2.17）：
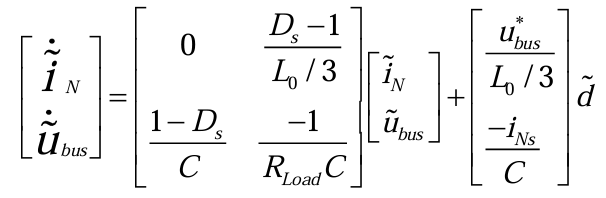
忽略输入电压的小信号扰动后，对（3.2.15）和（3.2.16）进行拉氏变换，得到（3.2.18）和（3.2.19）：
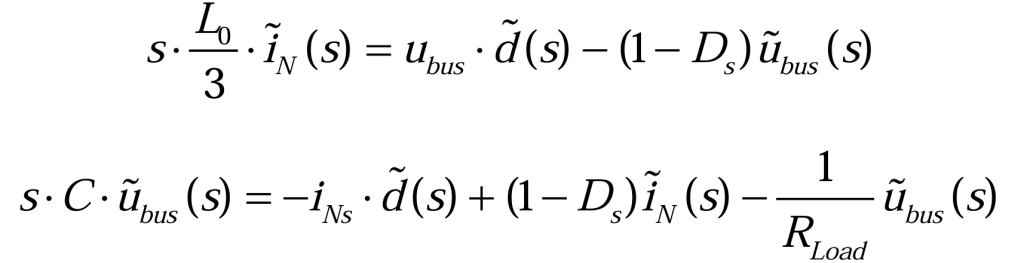
对（3.2.18）和（3.2.19）进行联立，消去共同变量d(s)，得到（3.2.20）：
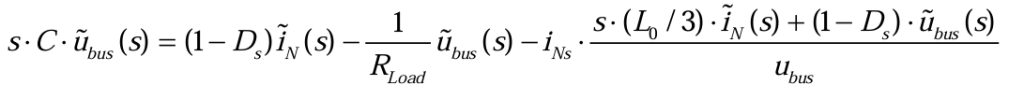
由表达式(3.2.2)，将iNs带入表达式(3.2.20)化简，整理可得(3.2.21)：
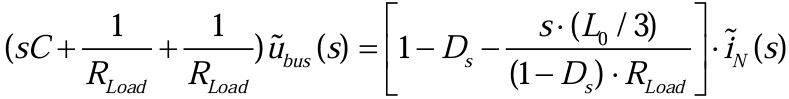
将表达式(3.2.2)带入表达式(3.2.21)，化简后可得母线电压到中性点电流的传递函数(3.2.22)*：【如下公式存在推导问题】
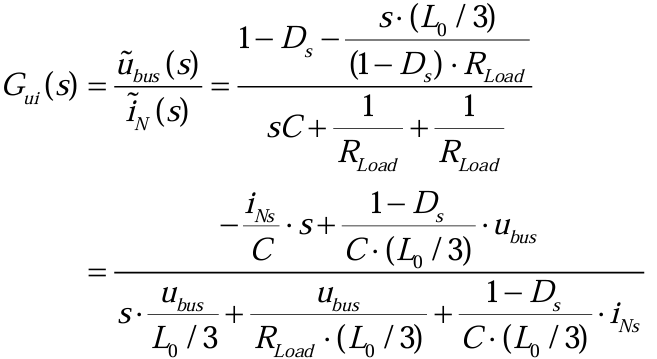
同理，由表达式(3.2.18)，得(3.2.23)*：
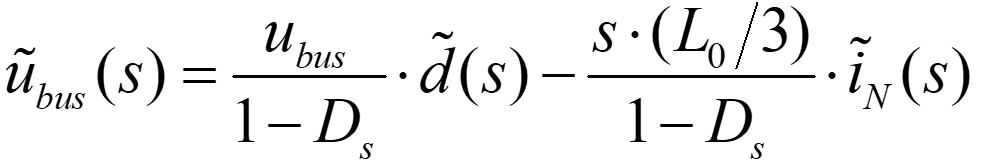
将表达式（3.2.2）和（3.2.23）代入（3.2.19），可以得到（3.2.24）*：
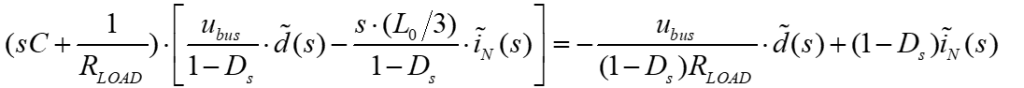
得中性点电流到占空比的传递函数（3.2.25）：
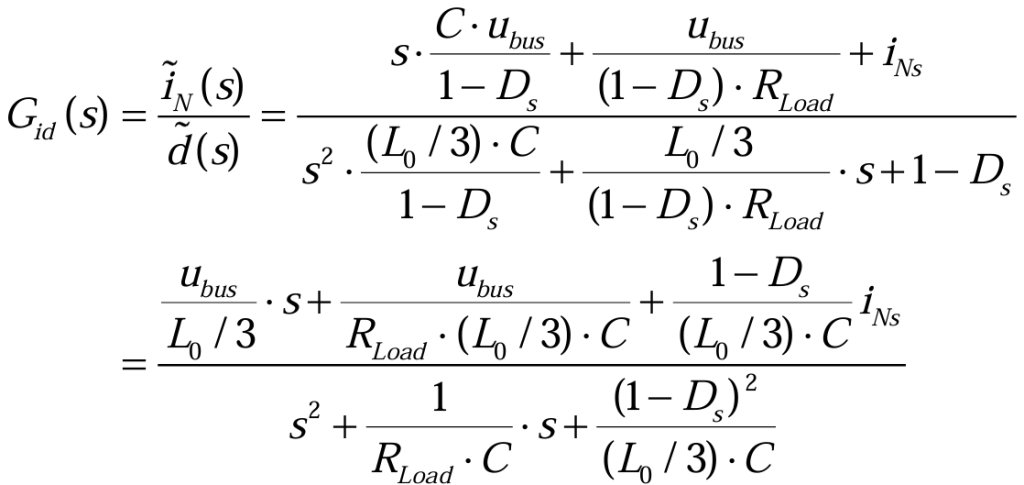
通过推导出的传递函数，调节DC/DC变换器部分的电压环和电流环PI参数，实现对母线电压的控制。
对等效DC/DC变换器进行闭环控制可以通过实时反馈调整系统的参数，来应对输入变化或负载需求的波动，确保等效 DC/DC 变换器的输出(直流母线电压)保持在预设的目标值附近，以保证电机能够稳定运行。闭环运行的控制框图如下：
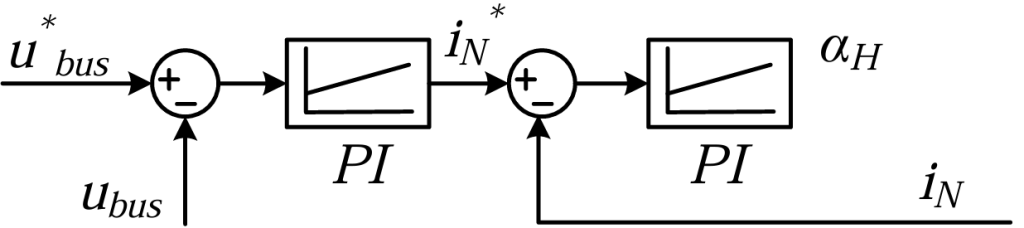
与永磁同步电机的双闭环控制系统原理一致，等效DC/DC变换器也采用了类似的双闭环控制思想。电压外环用于控制直流母线电压的大小。输入信号是直流母线电压给定值与实际电压之差，通过 PI调节器消除误差，确保系统在不同负载下母线电压的稳定性，并输出中性点电流的给定值。电流内环用于更精确地控制电流。输入信号是电压回路输出的中性点电流给定值与实际值之差，输出信号为逆变器的平均占空比H。PI 控制器根据电流误差调节输出的逆变器平均占空比，实现对直流母线电压的精确控制，进而优化电机的性能和能效。对等效 DC/DC 变换器采用闭环控制时，稳定时输出的逆变器平均占空比H只与直流母线电压的给定值和中性点电压有关。
3.3零序电压注入脉冲宽度调制策略(ZSVIPWM)
调制策略上，由于SVPWM算法会导致直流母线电压波动过大，无法有效地控制电压稳定，因此传统的SVPWM并不适用于中性点供电的方案，在此提出了新的调制方案——ZSVIPWM（零序电压注入式脉冲宽度调制）
①零序电压和占空比的计算
中性点供电方案需要一定的零序电压，所需的零序电压分量为(3.3.1)：
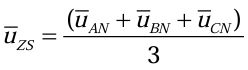
结合图3，综合看式（2.2.8）（2.2.12）和（3.3.1），得到式（3.3.2）：
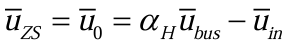
注入零序之后的实际相电压参考值为（3.3.3）：
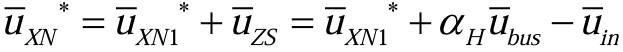
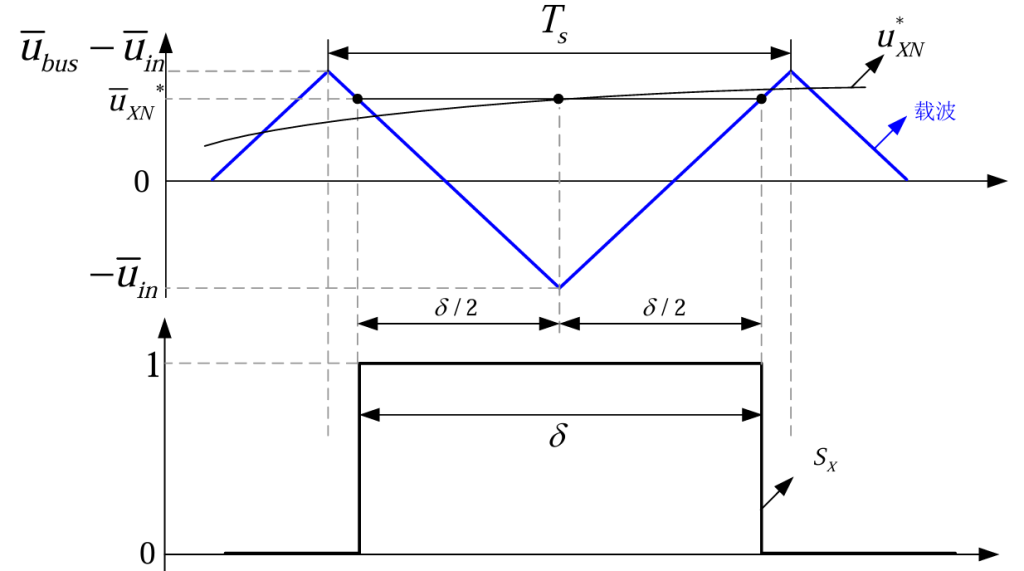
由于中性点电位被钳位，根据图3所示电路，当桥臂上半部分的开关管SA、SB和SC闭合时，永磁同步电机上的相电压为ubus-uin。当桥臂下半部分的开关管SA‘、SB‘和SC‘闭合时，永磁同步电机上的相电压为-uin。因此中性点供电拓扑结构中载波信号的正负幅值分别为ubus-uin和-uin。
根据规则采样法，如图10所示，可以得到逆变器开关管的占空比（3.3.4）：【规则采样法具体见附录】
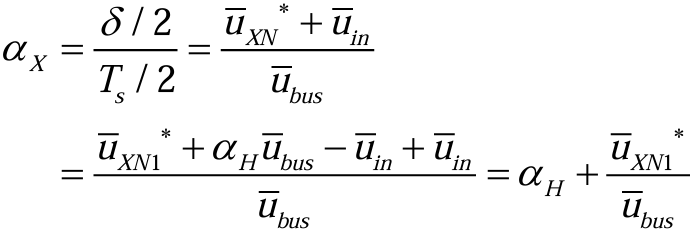
其中，δ为一个PWM周期内Sx的高电平时间。公式就是ZSVIPWM的最终算法。H通过控制等效DC/DC变换器的升压比，进而控制直流母线电压的大小。uXN1作为电机电压的参考值控制电机的运行。ZSVIPWM实现了对母线电压和电机运行的控制。
对如图1 所示的传统三相两电平逆变器驱动的三相永磁同步电机来说，如果采用SPWM，当桥臂上半部分的开关管Sn闭合时，永磁同步电机上的相电压为0.5uin。当桥臂下半部分的开关管Sn‘闭合时，永磁同步电机上的相电压为−0.5uin。因此传统拓扑的中载波信号的正负幅值分别为0.5uin和−0.5uin。同理，根据规则采样法，可以得到逆变器开关管的占空比：
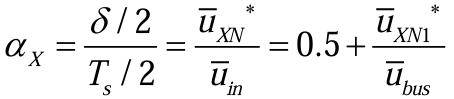
附录部分
规则采样法解释：
要介绍规则采样法，先需要明白自然采样法。在通常情况下，按照SPWM控制的基本原理，在正弦波和三角波的交点时刻控制功率开关器件的通断，这种生成SPWM的方法称为自然采样法。
自然采样法是最基本的采样方法，由此得到的SPWM波形也很接近正弦波。但此方法需要求解复杂的超越方程，采用微机控制时需花费大量的计算时间，难以实现实时控制，所以应用不多。
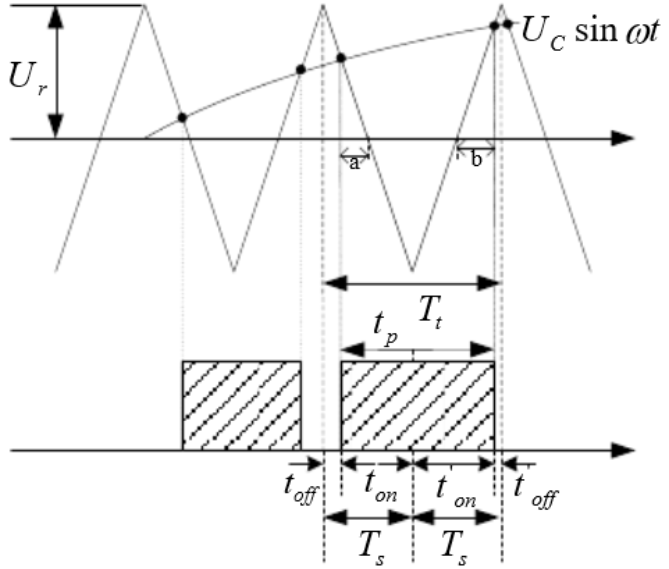
对称规则采样法本质是在三角波的顶点位置或者底点位置对正弦波采样而形成阶梯波，利用该阶梯波来与载波（三角波）相交，由交点来得出脉冲宽度。此阶梯波与三角波的交点所确定的脉宽在一个采样周期（这里，Ts=Tt）内的位置是对称的，故称为对称规则采样。由附图2所示：
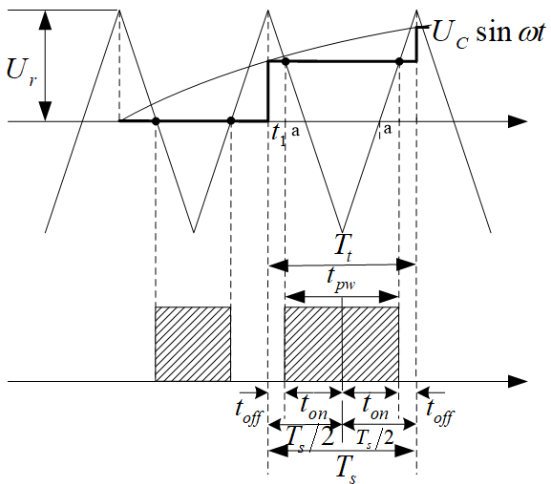
补充非对称采样法——其本质是在三角波的顶点位置和者底点位置对正弦波采样而形成更为密集的阶梯波，利用该阶梯波来与载波（三角波）相交，由交点来得出脉冲宽度。它在一个三角波的周期内的位置是不对称的，因此这样的方法称为不对称规则采样。这里采样周期是三角波周期的1/2，即Ts= Tt/2。
【以上内容来自CSDN——自然采样法，规则采样法和不规则采样法原理与区别】
参考文献：
