由于后需要开展中性点供电双电驱容错控制方面的研究,现推导一下中性点供电拓扑的开路容错控制。
众所周知,在正常工况下的三相永磁同步电机中,A、B和C相的相电流是呈正弦形状且互差120°的。当一相出现了绕组开相的故障(假设A相出现开路故障),则若依然控制正常相(B相和C相)为精准正弦,那么是不可能保证转矩为常数的。因此,B相和C相的形状应该是非规范正弦的。此外,为了保证转矩在故障前后保持不变,则q轴电流应该保持不变。因此,更改d轴电流成为了一种理论上的可能。接下来进行逐步分析——
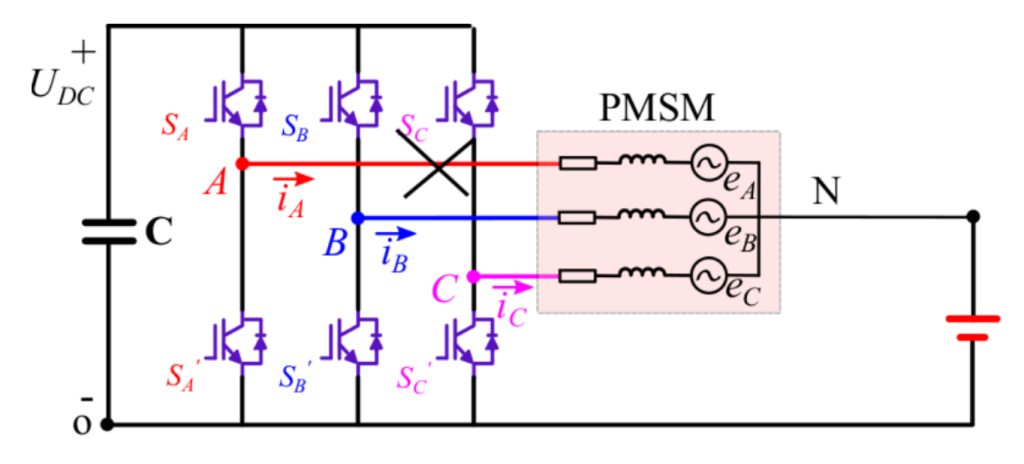
图示为开路故障下的中性点供电拓扑的结构示意图:
由Park变换,得(1)式:
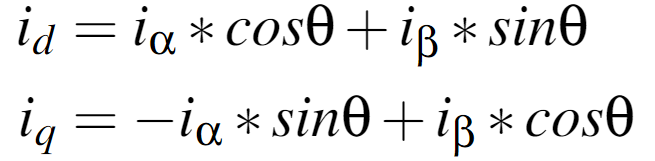
当A相发生开路故障时,由于零序电流存在
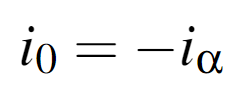
将(2)代入(1)得到(3)式:
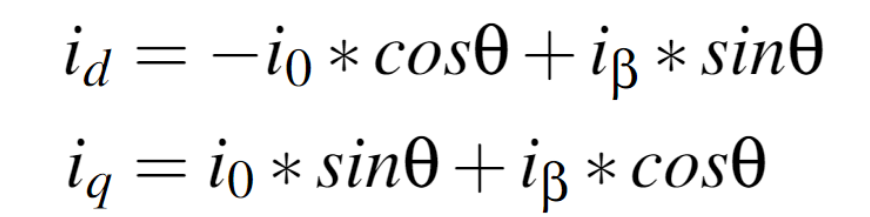
将iqh定义为健康状况下的q轴电流,为了保证转矩为常数,必须保证故障前后的q轴电流保持不变,即iq=iqh,因此在故障条件下,可以得到(4)式:
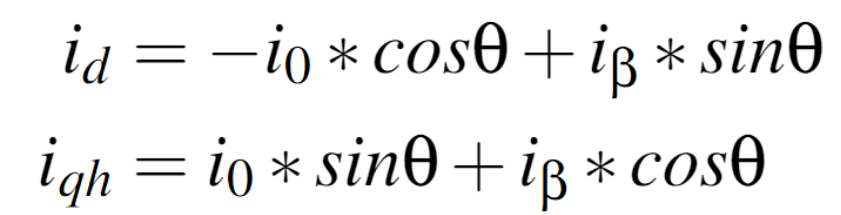
化简(4),可以得到(5):(消除beta)
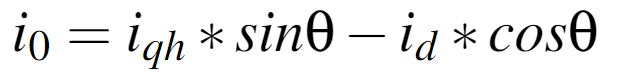
根据(5),其实我们已经知道了id、iqh和i0的关系了,也就是说,如果我们知道了i0,我们就可以计算id。实际上,id是重新调整iB和iC的自由度。在这种情况下,电机通常会出现弱磁和增磁的情况。
由于我们希望在故障前后保持扭矩和速度恒定,因此,输出功率一般来说也是恒定的。然而,为了保证iq=iqh,那么输入电流iin肯定不是常数了。再由于Pin=iin*uin,iin=-3*i0,这就意味着暂态的输入功率Pin不是恒定的。因此直流链路电容必须在一个周期内吸收或释放一些暂态功率。如果我们保持输入功率的平均值不变,则输出功率可以是恒定的。换句话说,如果我们在一个电气周期(θ = 2π)中保持i0的平均值是恒定的(i0平均值=i0h),我们可以保持转矩常数。因此,我们令(6)式:
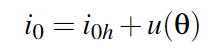
理论上,u(θ)可以是正弦信号或任意平方信号,我们假设:u(θ)=i0h*sinθ,把(6)代入(5)则有(7):
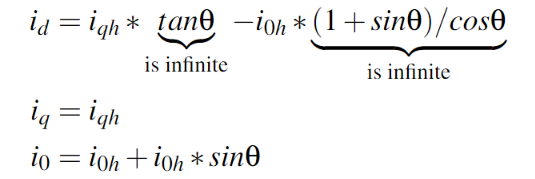
在实际的应用中,(7)式是无法实现的,因为id会变成无穷大,会导致磁饱和。因此,id 和 i0 必须是有界函数。根据(5),我们可以得到(8):
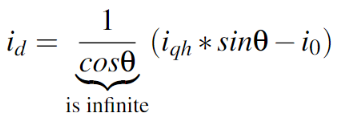
在(8)中,由于1/cos这个部分是发散的,因此我们不得不进行消除,我们令i0为(9):
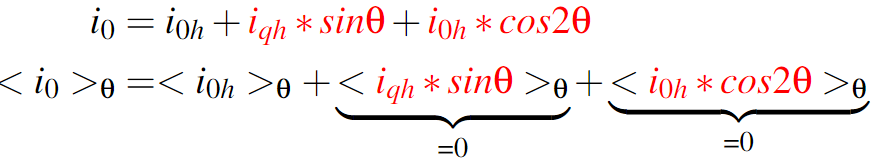
因此,将(9)代入(8),可以得到故障条件下的参考电流(10)。
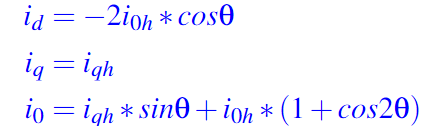
显然,id 和 i0 都是有界函数。因此,在故障后,如果我们将id、iq和i0控制为(10),电机可以保持转矩不变。




