基于矢量空间解耦的双三相永磁同步电机模型这部分真的很久没有更新了(都快一年了,这一年杂七杂八的忙碌了很多,现在课题方向也不再是双三相电机控制了,不过还是想把之前做过的工作好好记录一下),其实之前已经写了部分,不过因为觉得介绍的结构顺序不太对,于是决定重新开头再写一次,第二篇就主要介绍双三相PMSM的矢量空间解耦——
第4部分:矢量空间解耦
前文提到过,双三相PMSM的两套绕组的中性点式隔离的,零序子空间的分量都为0,在此可以忽略不计。根据上文的TDQ可以通过计算得到在dq坐标系下d-q子空间的电压方程:
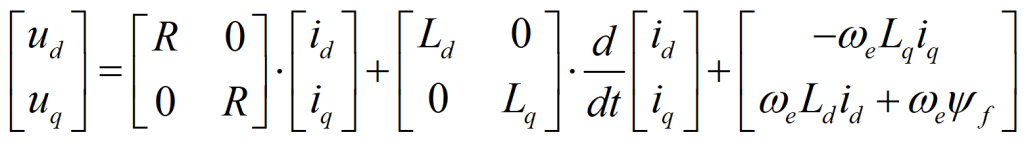
在dq坐标系下x-y子空间的电压方程:
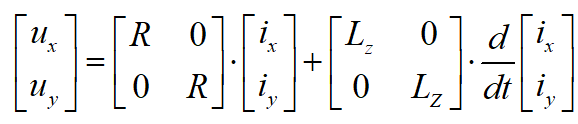
其中,ud、uq、ux、uy分别为d-q和x-y子空间的定子电压;id、iq、ix、iy分别为d-q和x-y子空间的定子电流;Ld、Lq为d-q坐标系下的电感;wc为电角速度。
根据新的变换矩阵,电磁转矩方程可简化为:
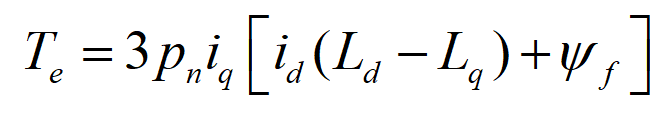
根据磁链和电流之间的关系,也可以将上式写成:
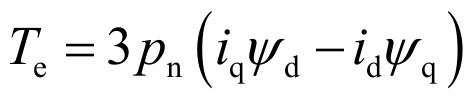
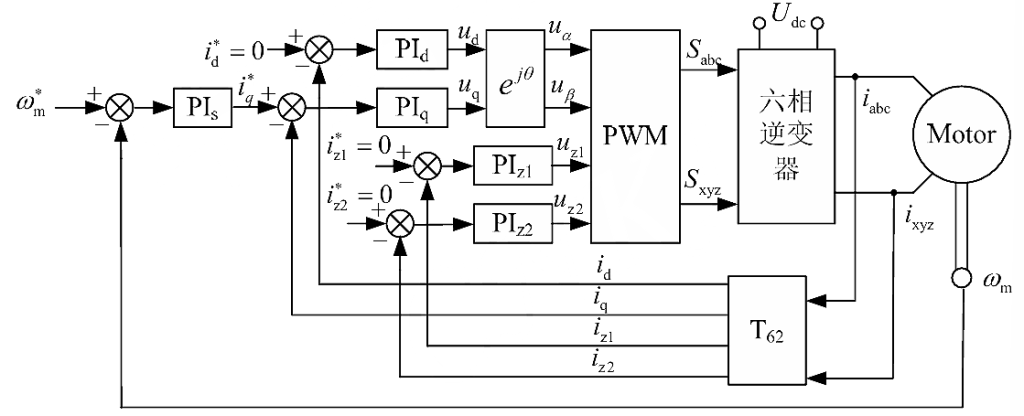
基于矢量空间解耦变换的双三相永磁同步电机转子磁场定向控制框图如上图所示。控制系统同样包括一个转速环和四个电流环。d-q子空间的控制与三相电机完全一致,此外还需要控制z1和z2轴的电流。电机总的定子铜耗可以表示为:
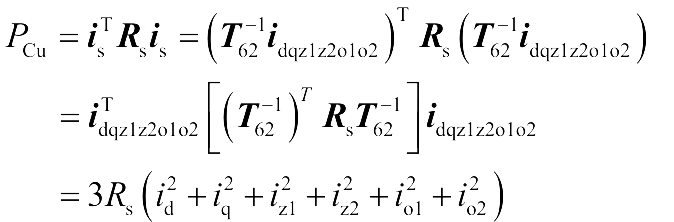
从式中可以看出,各相的定子铜耗之和亦等于新坐标系下各轴的定子铜耗之和。由于z1-z2、o1-o2子空间中的电流对于电磁转矩的产生没有任何贡献,只会增加定子铜耗,应该将其给定值都设为零,这样可以保证电机在输出相同电磁转矩时具有最小的定子铜耗。
当双三相电机采用隔离中性点时,o1-o2子空间的电流由连接方式决定了必然为零而不需要再进行控制。从矢量空间解耦模型中还可以看出,只要给定电压uz1和uz2为零,z1-z2子空间就不会产生电流,所以z1-z2子空间的电流完全可以进行开环控制,只要将其给定电压设为零即可,这样系统中就只有两个电流环,可以简化系统的结构。
但是,这只是理论分析的结果。以上为了建模的需要,对电机系统做了一些理想的假设,忽略了一些次要因素。在实际系统中,z1-z2子空间的电流并不完全由给定电压决定,由于一些未建模因素的影响,如谐波磁链、互漏感等,在电压方程中会耦合进一定的感应电动势,这些感应电动势的值可能非常小,但是由于z1-z2子空间的阻抗也很小,所以最后仍会产生的一定的电流。因此从定子铜耗最小的角度来说,z1-z2子空间的电流闭环还是需要的,未建模部分的影响可以视为扰动量用调节器来克服。
第5部分:simulink仿真分析部分
参照Matlab/Simulink 中三相永磁同步电机的数学模型,这里分别搭建了基于空间适量解耦模型的双三相永磁同步电机的仿真。
控制部分(使用svpwm算法):
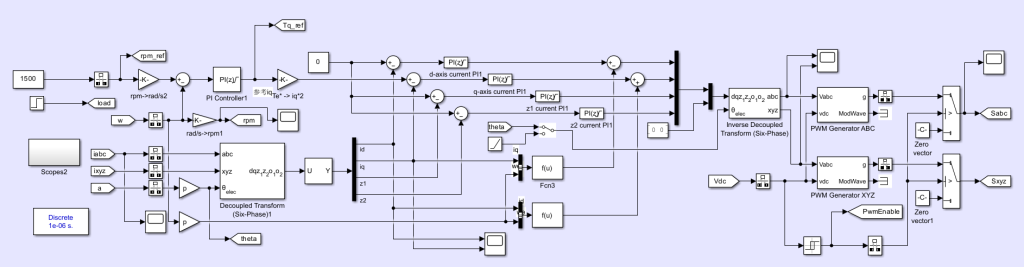
电机部分:
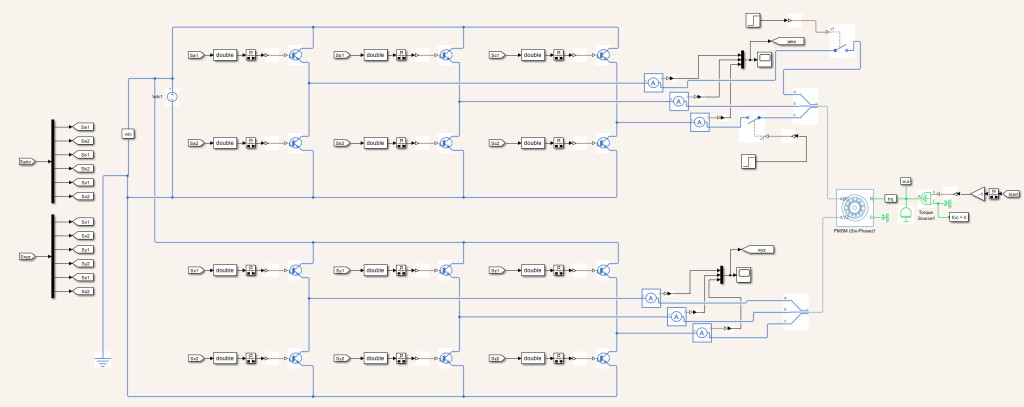
控制性能如下图所示(0.05s加入5N·m负载):
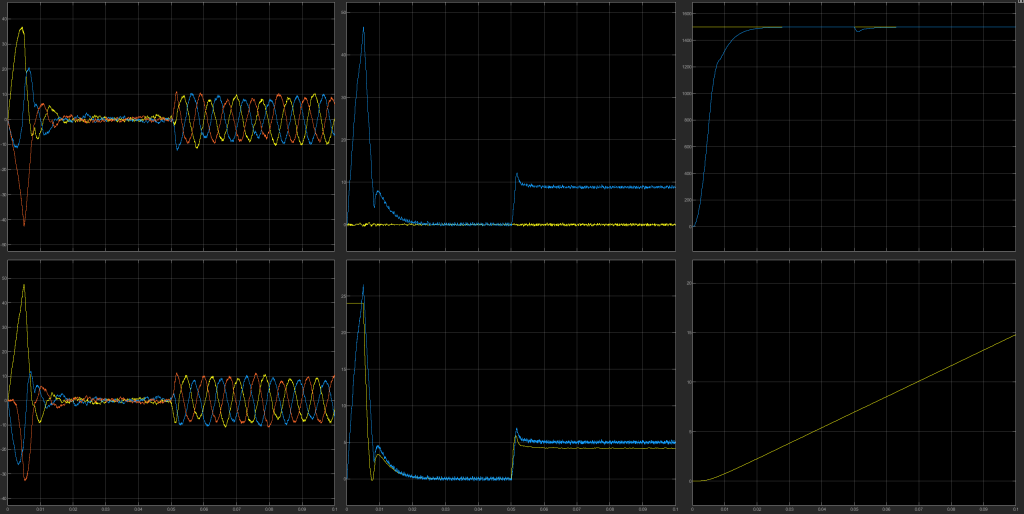
第一列两张图为abc侧三相电流和xyz侧三相电流;第二列上侧图为d-q轴电流,下侧图为转矩参考值和实际值;第三列上侧图为电机参考转速和实际转速,下侧图为电机机械角度。
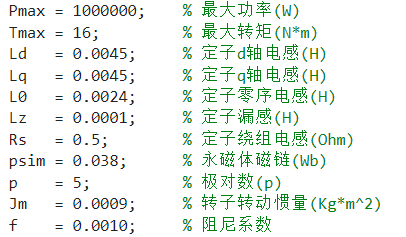
模型所选取的电机参数如下所示:
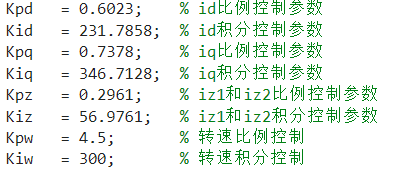
控制参数如下所示:
文献参考:
[1] 杨金波。双三相永磁同步电机建模与矢量控制 [D]. 哈尔滨:哈尔滨工业大学,2011.





哥哥好厉害啊
么么么